Ejemplos De Árboles Binarios De Búsqueda Para Entender Su Funcionamiento

Los árboles binarios de búsqueda son estructuras de datos fundamentales en la informática, utilizadas para organizar y gestionar información de manera eficiente. En este artículo, exploraremos diversos ejemplos prácticos que ilustran el funcionamiento y las aplicaciones de estos árboles en diferentes contextos. A medida que avancemos, descubrirás cómo su diseño optimizado permite realizar operaciones de búsqueda, inserción y eliminación con una notable eficacia.

Acompáñanos en este recorrido por el fascinante mundo de los árboles binarios de búsqueda y aprende a implementar estas técnicas en tus proyectos.

¿Qué es un árbol de búsqueda binario con un ejemplo?

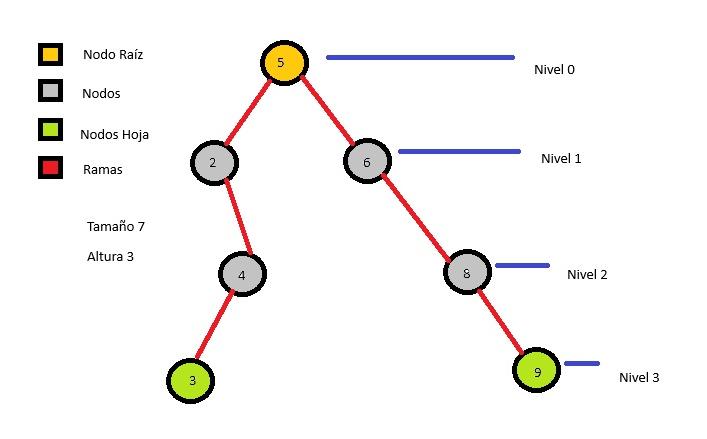
Un árbol de búsqueda binario es una estructura de datos en la que cada nodo tiene como máximo dos hijos (izquierdo y derecho) y cada nodo representa una clave o valor. La clave del nodo izquierdo es menor que la clave del nodo padre, mientras que la clave del nodo derecho es mayor que la clave del nodo padre. Esto permite una búsqueda eficiente de un valor específico en el árbol. Ejemplo: Supongamos que tenemos un árbol de búsqueda binario con los siguientes nodos: 8 / 3 10 /
1 6 14 / / 4 7 13 En este ejemplo, el nodo raíz es 8, y los nodos hijos de 8 son 3 y 10. El nodo 3 tiene dos hijos, 1 y 6, mientras que el nodo 10 tiene un hijo, 14.

Características de un árbol de búsqueda binario

Un árbol de búsqueda binario tiene las siguientes características:

1. Cada nodo tiene como máximo dos hijos: izquierdo y derecho.
2. La clave del nodo izquierdo es menor que la clave del nodo padre.
3. La clave del nodo derecho es mayor que la clave del nodo padre.

Ventajas de un árbol de búsqueda binario

Un árbol de búsqueda binario tiene las siguientes ventajas:

1. Búsqueda eficiente: un árbol de búsqueda binario permite una búsqueda eficiente de un valor específico en el árbol.
2. Inserción y eliminación eficientes: un árbol de búsqueda binario permite la inserción y eliminación eficientes de nodos.
3. Uso eficiente del espacio: un árbol de búsqueda binario puede almacenar un gran número de nodos en un espacio relativamente pequeño.

Aplicaciones de un árbol de búsqueda binario

Un árbol de búsqueda binario tiene las siguientes aplicaciones:

1. Bases de datos: un árbol de búsqueda binario se utiliza en bases de datos para indexar y buscar datos.
2. Sistemas de archivo: un árbol de búsqueda binario se utiliza en sistemas de archivo para organizar y buscar archivos.
3. Compiladores: un árbol de búsqueda binario se utiliza en compiladores para analizar y buscar símbolos en el código fuente.

¿Cómo funciona un árbol binario de búsqueda?

Un árbol binario de búsqueda (ABB) es una estructura de datos que se utiliza para almacenar y buscar datos de manera eficiente. Se compone de nodos, cada uno de los cuales tiene un valor y dos hijos: el hijo izquierdo y el hijo derecho. Cada nodo representa una clave o un valor que se utiliza para buscar y recuperar datos.

Estructura de un Árbol Binario de Búsqueda

La estructura de un ABB se basa en la siguiente regla: para cada nodo, todos los valores en el subárbol izquierdo son menores que el valor del nodo, y todos los valores en el subárbol derecho son mayores que el valor del nodo. Esto permite que se pueda buscar un valor de manera eficiente, ya que se puede descartar la mitad del árbol en cada paso.

1. Cada nodo tiene un valor único.
2. Cada nodo tiene dos hijos: el hijo izquierdo y el hijo derecho.
3. El subárbol izquierdo de un nodo contiene valores menores que el valor del nodo.

Operaciones en un Árbol Binario de Búsqueda

Un ABB admite varias operaciones, incluyendo la inserción, la búsqueda y la eliminación de nodos. La inserción se realiza agregando un nuevo nodo al árbol, y la búsqueda se realiza recorriendo el árbol hasta encontrar el nodo que se busca. La eliminación se realiza encontrando el nodo que se quiere eliminar y reemplazándolo con su hijo izquierdo o derecho.

1. Inserción: agregar un nuevo nodo al árbol.
2. Búsqueda: encontrar un nodo en el árbol.
3. Eliminación: eliminar un nodo del árbol.

Ventajas y Desventajas de un Árbol Binario de Búsqueda

Un ABB tiene varias ventajas, incluyendo la búsqueda eficiente y la capacidad de almacenar grandes cantidades de datos. Sin embargo, también tiene algunas desventajas, como la complejidad de la implementación y la necesidad de mantener el equilibrio del árbol.

1. Ventajas:
   • Búsqueda eficiente.
   • Capacidad de almacenar grandes cantidades de datos.
2. Desventajas:
   • Complejidad de la implementación.
   • Necesidad de mantener el equilibrio del árbol.

¿Qué aplicaciones tienen los árboles binarios de búsqueda?

Los árboles binarios de búsqueda son una estructura de datos fundamental en la informática, ya que permiten almacenar y recuperar información de manera eficiente. Esto se debe a que los árboles binarios de búsqueda están ordenados de tal manera que todos los elementos a la izquierda de un nodo son menores que el nodo, y todos los elementos a la derecha son mayores.

Aplicaciones en bases de datos

Los árboles binarios de búsqueda se utilizan ampliamente en bases de datos para indexar y recuperar información. Esto se debe a que los árboles binarios de búsqueda permiten una búsqueda rápida y eficiente de los datos. Algunas de las aplicaciones de los árboles binarios de búsqueda en bases de datos son:

1. Indexación: Los árboles binarios de búsqueda se utilizan para crear índices en las bases de datos, lo que permite una búsqueda rápida y eficiente de los datos.
2. Recuperación de datos: Los árboles binarios de búsqueda se utilizan para recuperar información de las bases de datos, ya que permiten una búsqueda rápida y eficiente de los datos.
3. Optimización de consultas: Los árboles binarios de búsqueda se utilizan para optimizar las consultas en las bases de datos, lo que permite una búsqueda rápida y eficiente de los datos.

Aplicaciones en algoritmos de ordenamiento

Los árboles binarios de búsqueda también se utilizan en algoritmos de ordenamiento para ordenar y clasificar información. Esto se debe a que los árboles binarios de búsqueda permiten una ordenación rápida y eficiente de los datos. Algunas de las aplicaciones de los árboles binarios de búsqueda en algoritmos de ordenamiento son:

1. Algoritmo de ordenamiento por árbol: Los árboles binarios de búsqueda se utilizan en el algoritmo de ordenamiento por árbol, que es un algoritmo de ordenamiento que utiliza un árbol binario de búsqueda para ordenar los datos.
2. Algoritmo de ordenamiento por selección: Los árboles binarios de búsqueda se utilizan en el algoritmo de ordenamiento por selección, que es un algoritmo de ordenamiento que utiliza un árbol binario de búsqueda para seleccionar los elementos a ordenar.
3. Algoritmo de ordenamiento por inserción: Los árboles binarios de búsqueda se utilizan en el algoritmo de ordenamiento por inserción, que es un algoritmo de ordenamiento que utiliza un árbol binario de búsqueda para insertar los elementos a ordenar.

Aplicaciones en sistemas de archivos

Los árboles binarios de búsqueda también se utilizan en sistemas de archivos para almacenar y recuperar información. Esto se debe a que los árboles binarios de búsqueda permiten una búsqueda rápida y eficiente de los datos. Algunas de las aplicaciones de los árboles binarios de búsqueda en sistemas de archivos son:

1. Sistemas de archivos jerárquicos: Los árboles binarios de búsqueda se utilizan en sistemas de archivos jerárquicos para almacenar y recuperar información.
2. Sistemas de archivos de red: Los árboles binarios de búsqueda se utilizan en sistemas de archivos de red para almacenar y recuperar información.
3. Sistemas de archivos distribuidos: Los árboles binarios de búsqueda se utilizan en sistemas de archivos distribuidos para almacenar y recuperar información.

¿Dónde se utiliza el árbol de búsqueda binaria en la vida real?

El árbol de búsqueda binaria es una estructura de datos fundamental en la informática que se utiliza en diversas aplicaciones de la vida real. A continuación, se presentan algunos ejemplos de dónde se utiliza el árbol de búsqueda binaria.

Bases de datos y sistemas de archivo

Los árboles de búsqueda binaria se utilizan en bases de datos y sistemas de archivo para organizar y recuperar datos de manera eficiente. Los árboles de búsqueda binaria permiten realizar búsquedas rápidas y precisas en grandes conjuntos de datos. Algunos ejemplos de cómo se utiliza el árbol de búsqueda binaria en bases de datos y sistemas de archivo son:

1. Índices de bases de datos: Los árboles de búsqueda binaria se utilizan para crear índices en bases de datos, lo que permite realizar búsquedas rápidas y precisas en grandes conjuntos de datos.
2. Sistemas de archivo: Los árboles de búsqueda binaria se utilizan en sistemas de archivo para organizar y recuperar archivos de manera eficiente.
3. Búsqueda de datos: Los árboles de búsqueda binaria se utilizan en algoritmos de búsqueda de datos para encontrar patrones y tendencias en grandes conjuntos de datos.

Compiladores y analizadores de código

Los árboles de búsqueda binaria se utilizan en compiladores y analizadores de código para analizar y procesar código fuente de manera eficiente. Los árboles de búsqueda binaria permiten realizar búsquedas rápidas y precisas en grandes conjuntos de código. Algunos ejemplos de cómo se utiliza el árbol de búsqueda binaria en compiladores y analizadores de código son:

1. Análisis léxico: Los árboles de búsqueda binaria se utilizan en el análisis léxico para identificar patrones y tokens en el código fuente.
2. Análisis sintáctico: Los árboles de búsqueda binaria se utilizan en el análisis sintáctico para analizar la estructura del código fuente y detectar errores.
3. Optimización de código: Los árboles de búsqueda binaria se utilizan en algoritmos de optimización de código para mejorar el rendimiento y la eficiencia del código generado.

Aplicaciones web y móviles

Los árboles de búsqueda binaria se utilizan en aplicaciones web y móviles para mejorar la experiencia del usuario y la eficiencia de la aplicación. Los árboles de búsqueda binaria permiten realizar búsquedas rápidas y precisas en grandes conjuntos de datos. Algunos ejemplos de cómo se utiliza el árbol de búsqueda binaria en aplicaciones web y móviles son:

1. Búsqueda de productos: Los árboles de búsqueda binaria se utilizan en aplicaciones de comercio electrónico para realizar búsquedas rápidas y precisas de productos.
2. Recomendaciones de contenido: Los árboles de búsqueda binaria se utilizan en aplicaciones de contenido para recomendar contenido relevante a los usuarios.
3. Autocompletado de texto: Los árboles de búsqueda binaria se utilizan en aplicaciones de texto para autocompletar palabras y frases mientras el usuario escribe.

### Ejemplos Prácticos de Árboles Binarios de Búsqueda: Comprendiendo su Estructura y Funcionamiento

Los árboles binarios de búsqueda (ABB) son una estructura de datos fundamental en la informática, utilizados para almacenar y organizar información de manera eficiente. Su principal característica es que cada nodo del árbol tiene como máximo dos hijos, y estos se organizan según un criterio: el valor del hijo izquierdo es siempre menor que el del nodo padre, mientras que el valor del hijo derecho es mayor.

Ejemplos Prácticos de Árboles Binarios de Búsqueda:

1. Organización de Datos: Un ABB permite insertar, buscar y eliminar elementos de forma rápida. Por ejemplo, si se desea mantener un registro de estudiantes por su número de identificación, se puede utilizar un ABB donde cada nodo representa a un estudiante. La búsqueda de un estudiante específico se realizaría siguiendo el criterio de menor o mayor, lo que optimiza el tiempo de búsqueda.

2. Visualización de Jerarquías: En aplicaciones de gestión empresarial, los ABB pueden ser útiles para representar jerarquías. Por ejemplo, un árbol que represente la estructura organizativa de una empresa, donde cada nodo representa a un empleado y sus subordinados, permite una navegación eficiente a través de la organización.

3. Base de Datos: Los ABB son ampliamente empleados en bases de datos para la indexación de registros. Cuando se busca un registro específico, el ABB facilita la localización del mismo sin necesidad de revisar toda la base de datos. Esto es especialmente útil en bases de datos grandes, donde el tiempo de acceso puede ser crítico.

4. Ordenamiento: Un árbol binario de búsqueda también puede ser utilizado para realizar un recorrido inorden (in-order traversal) que devuelve los elementos en orden ascendente. Este método de ordenamiento es eficiente y sencillo, permitiendo organizar elementos de manera efectiva.

Funcionamiento:

El funcionamiento de los árboles binarios de búsqueda se basa en tres operaciones fundamentales:

• Inserción: Para insertar un nuevo elemento, se comienza en la raíz y se compara el valor con el nodo actual. Si es menor, se avanza al subárbol izquierdo; si es mayor, al subárbol derecho. Este proceso se repite hasta encontrar un lugar vacío para el nuevo nodo.
• Búsqueda: Similar al proceso de inserción, se compara el valor buscado con el nodo actual y se avanza hacia el subárbol correspondiente hasta encontrar el elemento o llegar a un nodo nulo.
• Eliminación: Este proceso es más complejo y se realiza en tres casos: eliminando un nodo hoja, un nodo con un solo hijo o un nodo con dos hijos, donde se debe encontrar el sucesor o predecesor para mantener la propiedad del ABB.

Conclusiones sobre el uso práctico de los ABB: En el contexto de programación y estructuras de datos, los árboles binarios de búsqueda ofrecen una solución clara y eficiente para manejar conjuntos de datos que requieren operaciones frecuentes de inserción y búsqueda. Su implementación y manipulación resultan esenciales en el desarrollo de algoritmos y en el diseño de sistemas informáticos que necesitan gestionar grandes volúmenes de datos.

113. Curso Python || Estructura de Datos || Árboles Binarios de Búsqueda

Definición de Árboles Binarios de Búsqueda

Concepto Básico

Un árbol binario de búsqueda (ABB) es una estructura de datos que organiza elementos en un formato jerárquico. En este tipo de árbol, cada nodo tiene como máximo dos hijos, denominados hijo izquierdo y hijo derecho. La característica principal que define a un árbol binario de búsqueda es que para cada nodo, todos los valores de los nodos en su subárbol izquierdo son menores que el valor del nodo padre, y todos los valores en el subárbol derecho son mayores.

Esta propiedad permite realizar búsquedas de manera eficiente. Al comparar un valor con el nodo actual, se puede decidir si continuar la búsqueda hacia la izquierda o la derecha del árbol. Esto reduce significativamente el número de comparaciones necesarias para encontrar un elemento específico en comparación con otras estructuras de datos, como listas desordenadas.

Estructura y Componentes

La estructura de un árbol binario de búsqueda se compone principalmente de nodos. Cada nodo contiene:

• Valor: El dato que almacena el nodo.
• Referencia al hijo izquierdo: Un puntero hacia el nodo que representa el menor valor.
• Referencia al hijo derecho: Un puntero hacia el nodo que representa el mayor valor.

Los nodos son conectados entre sí de tal manera que forman una jerarquía. El nodo más alto en el árbol se denomina raíz, y a partir de él se pueden derivar otros nodos. Esta estructura permite que las operaciones de inserción, eliminación y búsqueda sean más rápidas en comparación con otras estructuras de datos.

Operaciones Comunes en Árboles Binarios de Búsqueda

Inserción de Elementos

La inserción en un árbol binario de búsqueda sigue un proceso específico. Comienza desde la raíz y se compara el valor a insertar con el valor del nodo actual. Dependiendo del resultado de la comparación, se decide si mover hacia el hijo izquierdo o el hijo derecho. Este proceso se repite hasta que se encuentra un nodo vacío donde se pueda insertar el nuevo valor.

El proceso de inserción se puede describir en los siguientes pasos:

• Iniciar desde la raíz del árbol.
• Comparar el valor a insertar con el nodo actual.
• Moverse hacia la izquierda si es menor o hacia la derecha si es mayor.
• Repetir hasta encontrar un nodo vacío.
• Insertar el nuevo nodo en ese lugar.

Este método asegura que la propiedad del árbol binario de búsqueda se mantenga después de la inserción y que el árbol siga siendo eficiente para futuras operaciones.

Búsqueda de Elementos

La búsqueda en un árbol binario de búsqueda es una operación que también se beneficia de su ordenamiento. Al igual que en la inserción, se comienza desde la raíz y se realizan comparaciones. Si el valor buscado es menor que el nodo actual, se continúa buscando en el subárbol izquierdo; si es mayor, se busca en el subárbol derecho.

Este proceso puede ser resumido en los siguientes pasos:

• Comenzar desde la raíz del árbol.
• Comparar el valor buscado con el nodo actual.
• Moverse hacia la izquierda o derecha según corresponda.
• Repetir hasta encontrar el nodo o determinar que el valor no está presente.

La eficiencia de esta operación es fundamental en aplicaciones donde se requiere acceso rápido a los datos. En un árbol balanceado, la búsqueda tiene una complejidad promedio de O(log n).

Ejemplo Práctico de un Árbol Binario de Búsqueda

Construcción de un Árbol

Para ilustrar cómo funciona un árbol binario de búsqueda, consideremos la inserción de los siguientes números: 15, 10, 20, 8, 12, 17, 25. Siguiendo el proceso de inserción mencionado anteriormente, el árbol se construye de la siguiente manera:

1. Se inserta 15 como la raíz.
2. Luego se inserta 10, que es menor que 15, por lo que se coloca a la izquierda.
3. A continuación, se inserta 20, que es mayor, colocándose a la derecha.
4. Continuando con 8, se coloca a la izquierda de 10.
5. Se inserta 12 a la derecha de 10.
6. Para 17, se coloca a la izquierda de 20.
7. Finalmente, 25 se coloca a la derecha de 20.

El árbol resultante se verá así:

“`
15
/
10 20
/ /
8 12 17 25
“`

Análisis del Árbol

En este árbol binario de búsqueda, se puede observar que cumple con todas las propiedades definitorias. Cada nodo tiene valores menores en su subárbol izquierdo y mayores en su subárbol derecho. Esto hace que las operaciones de búsqueda e inserción sean eficientes.

Además, dado que el árbol no está completamente balanceado, podría ser necesario aplicar técnicas de balanceo en casos donde se realicen muchas inserciones y eliminaciones para evitar que se degrade a una lista enlazada, lo que afectaría negativamente el rendimiento.

Aplicaciones de Árboles Binarios de Búsqueda

Uso en Bases de Datos

Los árboles binarios de búsqueda tienen aplicaciones significativas en el campo de las bases de datos. Son utilizados en sistemas de gestión de bases de datos para permitir búsquedas rápidas de registros. Las operaciones de inserción y eliminación permiten que los datos se mantengan organizados, lo cual es crucial para la eficiencia en el acceso a la información.

Además, muchas bases de datos utilizan estructuras de árbol como B-trees o AVL trees, que son variaciones de los árboles binarios de búsqueda que aseguran un balanceo adecuado, optimizando aún más las operaciones de búsqueda.

Otras Aplicaciones

Además de su uso en bases de datos, los árboles binarios de búsqueda se usan en diversas áreas, tales como:

• Inteligencia Artificial: Para construir árboles de decisión y facilitar la toma de decisiones basada en múltiples criterios.
• Compiladores: En la implementación de estructuras de datos que permiten la optimización del código.
• Sistemas de Archivos: Para organizar y acceder eficientemente a grandes volúmenes de datos.

En resumen, los árboles binarios de búsqueda son herramientas fundamentales en la informática moderna, proporcionando una base sólida para el manejo y la organización de la información.

Preguntas Frecuentes

¿Cuáles son las características fundamentales de un árbol binario de búsqueda y cómo se manifiestan en ejemplos prácticos?

Un árbol binario de búsqueda (ABB) tiene características fundamentales que son esenciales para su funcionamiento:

1. Estructura jerárquica: Cada nodo tiene como máximo dos hijos, uno izquierdo y uno derecho.
2. Ordenación: Para cada nodo, todos los valores en el subárbol izquierdo son menores y en el derecho son mayores.
3. Búsqueda eficiente: Permite buscar, insertar y eliminar nodos en O(log n) en promedio.

Ejemplo práctico: En un sistema de gestión de inventarios, un ABB puede organizar productos por código, facilitando la búsqueda rápida de un artículo específico. Si se busca un producto con código “C123”, el árbol permite descartar rápidamente la mitad de los elementos, haciendo la búsqueda más eficiente.

¿Qué ejemplos ilustran la eficiencia en la búsqueda, inserción y eliminación de nodos en un árbol binario de búsqueda?

En un árbol binario de búsqueda, la eficiencia en las operaciones se puede ilustrar con los siguientes ejemplos:

1. Búsqueda: Si buscamos un nodo con valor 15 y el árbol está balanceado, se requerirán a lo sumo log₂(n) comparaciones, donde n es el número de nodos.

2. Inserción: Al insertar un nuevo nodo con valor 12, comenzaremos en la raíz y, dependiendo de su valor, seguiremos hacia la izquierda o derecha, de nuevo haciendo un máximo de log₂(n) movimientos si el árbol está balanceado.

3. Eliminación: Para eliminar un nodo (por ejemplo, el nodo con valor 20), se requiere encontrarlo primero, lo que también toma log₂(n) tiempo, seguido de reestructurar el árbol, manteniendo su propiedad de búsqueda.

Estos ejemplos muestran cómo, en un árbol balanceado, cada operación se realiza en tiempo O(log n).

¿Cómo se comparan diferentes ejemplos de árboles binarios de búsqueda en términos de complejidad temporal y espacial?

Los árboles binarios de búsqueda (ABB) se comparan en complejidad temporal y espacial según su estructura. En un ABB balanceado, como el AVL o el Rojo-Negro, las operaciones de búsqueda, inserción y eliminación tienen una complejidad temporal de O(log n), mientras que en un ABB desbalanceado, la complejidad puede degradarse a O(n). En términos de complejidad espacial, ambos tipos requieren O(n) para almacenar los nodos, pero un ABB desbalanceado puede ocupar más espacio en la pila durante operaciones recursivas debido a su profundidad.

¿Qué casos de uso específicos ejemplifican la aplicación de árboles binarios de búsqueda en la resolución de problemas computacionales?

Los árboles binarios de búsqueda se utilizan en varios casos de uso específicos, tales como:

1. Búsqueda eficiente: Permiten realizar búsquedas rápidas en conjuntos de datos desordenados.
2. Inserción y eliminación de datos: Facilitan la inserción y eliminación de elementos manteniendo el orden.
3. Implementación de bases de datos: Son usados en sistemas de gestión de bases de datos para indexar registros.
4. Algoritmos de ordenación: Se pueden utilizar en algoritmos como el tree sort para ordenar elementos.

Estos ejemplos ilustran cómo los árboles binarios de búsqueda optimizan diversas operaciones en la computación.

En conclusión, los árboles binarios de búsqueda son estructuras fundamentales en la informática, facilitando una búsqueda eficiente de datos. Comprender sus ejemplos y aplicaciones es crucial para el desarrollo de algoritmos. Te invitamos a compartir este contenido y seguir explorando más sobre este apasionante tema. ¡Tu conocimiento es clave!