El rombo, figura geométrica de cuatro lados iguales y dos pares de ángulos congruentes, es objeto de estudio en diversas disciplinas. En este artículo, exploraremos ejemplos concretos que ilustran su aplicación en matemáticas, física, ingeniería y más. Descubre cómo el rombo despliega sus propiedades únicas y complejas en distintos contextos académicos. ¡Sumérgete en el fascinante mundo del rombo y amplía tus conocimientos con ejemplos reveladores!
Contenido
- ¿Cuales son ejemplos de rombo?
- ¿Cómo es el rombo en figuras geométricas?
- ¿Dónde puedes encontrar un rombo en la vida real?
- ¿Qué simboliza el rombo?
- Ejemplos prácticos y claros del Rombo: ¡Descubre su versatilidad geométrica!
- Falsa suposición – método del rombo
- Tensión en el aire: el Reino Unido interceptó dos bombarderos rusos
- Ejemplos de Rombo en Geometría
- Preguntas Frecuentes
¿Cuales son ejemplos de rombo?

Un rombo es un tipo de cuadrilátero con lados iguales y ángulos opuestos iguales. A continuación, se presentan algunos ejemplos de rombos:
Ejemplos de rombos en la vida cotidiana
Un rombo se puede encontrar en diversas formas y objetos en la vida diaria. Algunos ejemplos incluyen:
- Las señales de tráfico en forma de rombo, utilizadas para indicar peligro o advertencia.
- Las baldosas y materiales de construcción que se colocan en patrones de rombo para crear diseños visuales interesantes.
- Los diseños de ropa y tejidos que incorporan patrones de rombo para agregar textura y estilo.
Ejemplos de rombos en la naturaleza
La naturaleza también presenta ejemplos de rombos en diversas formas y estructuras. Algunos ejemplos incluyen:
- Las formaciones de rocas y minerales que se cristalizan en patrones de rombo.
- Las escamas de peces y caparazones de tortugas que presentan patrones de rombo para la protección y defensa.
- Las flores y hojas que presentan patrones de rombo en su estructura y disposición.
Ejemplos de rombos en el arte y la arquitectura
El arte y la arquitectura también han incorporado el rombo en sus diseños y estructuras. Algunos ejemplos incluyen:
- Las iglesias y catedrales que presentan patrones de rombo en sus vidrieras y mosaicos.
- Los edificios y monumentos que incorporan patrones de rombo en sus diseños y estructuras.
- Las obras de arte que utilizan el rombo como tema o patrón en sus composiciones.
¿Cómo es el rombo en figuras geométricas?

El rombo es una figura geométrica cuadrilátera que se caracteriza por tener cuatro lados de igual longitud y ángulos opuestos que son iguales. Esto significa que los ángulos adyacentes del rombo son suplementarios, es decir, que suman 180 grados. El rombo también tiene dos diagonales que se bisecan en ángulos rectos, lo que significa que se cortan en dos partes iguales.
Propiedades del Rombo
El rombo tiene varias propiedades interesantes que lo hacen único entre las figuras geométricas. A continuación, se presentan algunas de las propiedades más importantes del rombo:
- Lados iguales: Todos los lados del rombo tienen la misma longitud.
- Ángulos opuestos iguales: Los ángulos opuestos del rombo son iguales.
- Diagonales bisecantes: Las diagonales del rombo se bisecan en ángulos rectos.
Tipos de Rombos
Existen varios tipos de rombos que se clasifican según sus propiedades y características. A continuación, se presentan algunos de los tipos más comunes de rombos:
- Rombo regular: Un rombo con todos sus lados y ángulos iguales.
- Rombo irregular: Un rombo con lados o ángulos desiguales.
- Rombo con ángulos rectos: Un rombo con dos ángulos rectos opuestos.
Aplicaciones del Rombo
El rombo tiene varias aplicaciones en diferentes campos, como la arquitectura, la ingeniería y el diseño. A continuación, se presentan algunas de las aplicaciones más comunes del rombo:
- Diseño de edificios: El rombo se utiliza en la arquitectura para crear diseños simétricos y estéticos.
- Ingeniería: El rombo se utiliza en la ingeniería para crear estructuras resistentes y estables.
- Diseño gráfico: El rombo se utiliza en el diseño gráfico para crear patrones y diseños geométricos.
¿Dónde puedes encontrar un rombo en la vida real?

Un rombo es una figura geométrica con cuatro lados iguales y paralelos dos a dos. Aunque puede parecer un concepto abstracto, los rombos se encuentran en diversas formas y objetos en la vida real.
Arquitectura y Diseño
Los rombos se utilizan comúnmente en la arquitectura y el diseño para crear patrones y formas visuales interesantes. Algunos ejemplos de dónde se pueden encontrar rombos en la arquitectura y el diseño incluyen:
- Pisos y azulejos: Los rombos se utilizan a menudo en la creación de patrones para pisos y azulejos, agregando un toque de elegancia y sofisticación a los espacios.
- Fachadas de edificios: Los rombos se pueden encontrar en la fachada de algunos edificios, creando un patrón geométrico que atrae la atención.
- Diseño de interiores: Los rombos se utilizan en el diseño de interiores para crear patrones y formas visuales interesantes en paredes, techos y muebles.
Naturaleza y Biología
La naturaleza también es una fuente rica en rombos. Algunos ejemplos de dónde se pueden encontrar rombos en la naturaleza y la biología incluyen:
- Cristales y minerales: Algunos cristales y minerales, como el cuarzo y el diamante, presentan formas geométricas que incluyen rombos.
- Flores y plantas: Algunas flores y plantas, como la flor de lis y el trébol, tienen patrones geométricos que incluyen rombos.
- Estructuras moleculares: Algunas moléculas, como la molécula de ADN, presentan formas geométricas que incluyen rombos.
Arte y Cultura
Los rombos también se encuentran en diversas formas de arte y cultura. Algunos ejemplos de dónde se pueden encontrar rombos en el arte y la cultura incluyen:
- Arte geométrico: El arte geométrico a menudo incorpora rombos y otras formas geométricas para crear patrones y formas visuales interesantes.
- Simbolismo: En algunas culturas, los rombos tienen un significado simbólico, como la representación de la unión y la armonía.
- Motivos textiles: Los rombos se utilizan comúnmente en la creación de motivos textiles, como en telas y alfombras.
¿Qué simboliza el rombo?
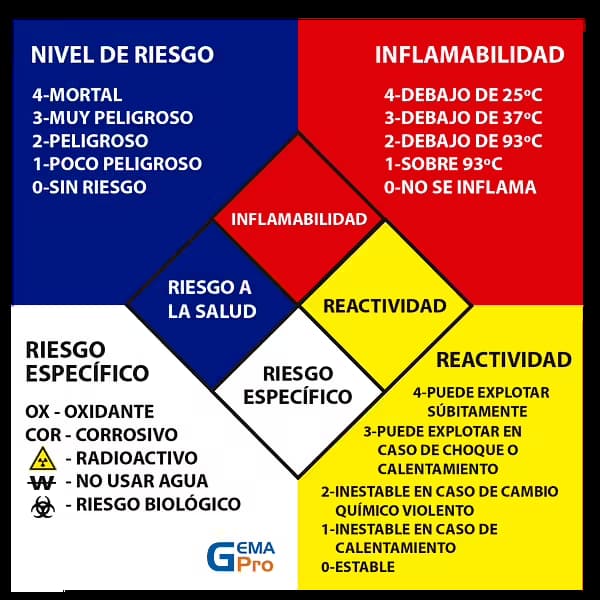
El rombo es un símbolo geométrico que ha sido utilizado en diversas culturas y contextos, y su significado puede variar dependiendo de la tradición y la aplicación.
Orígenes y significado en la geometría
El rombo es un cuadrilátero con lados iguales y ángulos opuestos iguales. En la geometría, el rombo se considera un símbolo de equilibrio y armonía, ya que sus lados y ángulos están en perfecta proporción. Algunos de los significados asociados con el rombo en la geometría son:
- Representa la unión de dos triángulos, lo que puede simbolizar la unión de dos fuerzas o principios opuestos.
- Se asocia con la cuadratura del círculo, lo que representa la búsqueda de la perfección y la armonía.
- Puede representar la dualidad, ya que tiene dos pares de lados iguales y dos pares de ángulos opuestos iguales.
Simbolismo en la cultura y la espiritualidad
En diversas culturas y tradiciones espirituales, el rombo se ha utilizado como símbolo de protección, fuerza y poder. Algunos de los significados asociados con el rombo en la cultura y la espiritualidad son:
- En la cultura africana, el rombo se asocia con la fertilidad y la prosperidad.
- En la tradición cristiana, el rombo se ha utilizado como símbolo de la cruz y la redención.
- En la cultura hindú, el rombo se asocia con el tercer ojo y la iluminación.
Uso en la heráldica y la simbología moderna
En la heráldica y la simbología moderna, el rombo se ha utilizado como símbolo de distinción y prestigio. Algunos de los significados asociados con el rombo en la heráldica y la simbología moderna son:
- Se utiliza como símbolo de nobleza y aristocracia en la heráldica.
- En la simbología masónica, el rombo se asocia con la sabiduría y la iluminación.
- En la cultura popular, el rombo se ha utilizado como símbolo de la originalidad y la independencia.
Ejemplos prácticos y claros del Rombo: ¡Descubre su versatilidad geométrica!
El rombo es una figura geométrica que posee características y propiedades únicas. A continuación, presentaremos algunos ejemplos prácticos y claros que ilustran la versatilidad de esta forma.
1. Identificación de un rombo:
– Un rombo se distingue por tener sus cuatro lados iguales en longitud.
– Sus ángulos internos son todos iguales, midiendo 90 grados cada uno.
– Los diagonales de un rombo se cortan en ángulos de 90 grados.
2. Aplicaciones en arquitectura:
– En el diseño arquitectónico, el rombo se utiliza para crear elementos decorativos en fachadas, como ventanas, balcones o molduras.
– También se puede utilizar como base para diseñar techos o cúpulas en edificios, aprovechando su forma simétrica y equilibrada.
3. Utilidad en la ingeniería:
– En la ingeniería civil, el rombo puede ser utilizado para diseñar estructuras metálicas, como puentes o torres de comunicación, debido a su resistencia y estabilidad.
– Además, en la geometría descriptiva, el rombo se emplea para representar objetos o planos inclinados en proyecciones ortogonales.
4. Uso en la joyería:
– En el ámbito de la joyería, el rombo se utiliza como base para la creación de colgantes, pendientes o anillos, ofreciendo un aspecto elegante y sofisticado.
– Además, se pueden combinar rombos de diferentes tamaños y materiales para crear diseños más complejos y llamativos.
En conclusión, el rombo es una figura geométrica versátil que se encuentra presente en diferentes áreas de nuestra vida cotidiana. Su forma equilibrada y simétrica lo convierte en un elemento estético y funcional en disciplinas como la arquitectura, la ingeniería y la joyería.
¡Descubre la versatilidad del rombo!
- Identificación de un rombo
- Un rombo tiene cuatro lados iguales
- Ángulos internos de 90 grados
- Diagonales que se cortan en ángulos de 90 grados
- Aplicaciones en arquitectura
- Diseño de elementos decorativos en fachadas
- Creación de techos o cúpulas
- Utilidad en la ingeniería
- Diseño de estructuras metálicas
- Representación de objetos en geometría descriptiva
- Uso en la joyería
- Creación de colgantes, pendientes o anillos
- Combinación de rombos para diseños más complejos
Falsa suposición – método del rombo
Tensión en el aire: el Reino Unido interceptó dos bombarderos rusos
Ejemplos de Rombo en Geometría
1. Características del rombo
El rombo es un cuadrilátero que se caracteriza por tener sus cuatro lados congruentes, es decir, de igual longitud. Además, sus diagonales también son segmentos congruentes y se cruzan perpendicularmente en su punto medio. Estas propiedades hacen del rombo una figura simétrica que puede encontrarse tanto en la naturaleza como en construcciones humanas.
Por ejemplo, el diamante es un cristal que tiene forma de rombo y se utiliza en joyería debido a su alto valor y belleza. Asimismo, algunos letreros de tráfico tienen forma de rombo para indicar advertencias o señales de peligro en la vía pública.
2. Área y perímetro del rombo
El área de un rombo puede ser calculada utilizando la fórmula A = (d1 * d2) / 2, donde d1 y d2 representan las longitudes de las diagonales del rombo. Por ejemplo, si conocemos que d1 = 6 cm y d2 = 8 cm, podemos calcular el área de la siguiente manera:
- Multiplicamos las longitudes de las diagonales: 6 cm * 8 cm = 48 cm².
- Dividimos el resultado entre 2: 48 cm² / 2 = 24 cm².
Por lo tanto, el área del rombo es de 24 cm².
En cuanto al perímetro del rombo, se puede calcular sumando las longitudes de sus cuatro lados. Si conocemos que los lados del rombo miden 5 cm cada uno, podemos calcular el perímetro de la siguiente manera:
- Sumamos las longitudes de los lados: 5 cm + 5 cm + 5 cm + 5 cm = 20 cm.
Por lo tanto, el perímetro del rombo es de 20 cm.
3. Aplicaciones del rombo en la arquitectura
El rombo es una figura geométrica ampliamente utilizada en la arquitectura debido a sus propiedades estéticas y estructurales. Por ejemplo, en la construcción de cúpulas o techos abovedados, el uso de rombos permite distribuir el peso de manera uniforme, lo que proporciona estabilidad y resistencia a la estructura.
Además, el uso de rombos en la arquitectura también puede ser apreciado en el diseño de ventanas, mosaicos y patrones decorativos en fachadas de edificios. Estas aplicaciones del rombo no solo cumplen una función estética, sino que también contribuyen a la integración visual de la estructura en su entorno.
En conclusión, el rombo es una figura geométrica que se encuentra presente en diferentes aspectos de nuestra vida cotidiana, desde la naturaleza hasta la arquitectura. Sus propiedades y características lo convierten en una figura relevante en el estudio de la geometría y su aplicación en diversos campos.
Preguntas Frecuentes
¿Cuáles son las características principales de un rombo y cuáles son algunos ejemplos de objetos o figuras geométricas que pueden ser considerados rombos?
Un rombo es un tipo de figura geométrica que se caracteriza por tener cuatro lados iguales y dos pares de ángulos opuestos iguales. Algunas características principales de un rombo son:
1. Lados iguales: Los cuatro lados de un rombo tienen la misma longitud, lo que significa que todos son iguales entre sí.
2. Ángulos iguales: Los dos pares de ángulos opuestos en un rombo son iguales entre sí. Esto significa que los ángulos interiores del rombo son congruentes, es decir, tienen la misma medida.
3. Diagonales perpendiculares: En un rombo, las diagonales son segmentos que unen los vértices opuestos. Estas diagonales siempre se intersectan en un ángulo de 90 grados, lo que significa que son perpendiculares entre sí.
Algunos ejemplos de objetos o figuras geométricas que pueden ser considerados rombos son:
1. Los diamantes: Los diamantes suelen tener forma de rombo, con sus cuatro lados iguales y ángulos opuestos congruentes. Por ejemplo, la joyería y algunos diseños de cartas de juego representan diamantes en forma de rombo.
2. Señales de tráfico: Algunas señales de tráfico tienen forma de rombo, como la señal de “Pare” o la señal de “Precaución”. Estas señales suelen tener cuatro lados iguales y ángulos opuestos congruentes.
3. Azulejos: Algunos azulejos decorativos tienen forma de rombo. Estos azulejos se pueden utilizar para crear patrones interesantes en paredes o pisos.
4. Algunos logotipos: Algunos logotipos utilizan la forma de un rombo para representar su marca. Por ejemplo, el logotipo de una empresa de joyería puede tener forma de rombo para transmitir elegancia y lujo.
Estos son solo algunos ejemplos de objetos o figuras geométricas que pueden ser considerados rombos. La versatilidad del rombo hace que se utilice en diversos contextos tanto en la vida cotidiana como en el diseño y la decoración.
¿Cuál es la fórmula para calcular el área de un rombo y cómo se aplica a diferentes ejemplos prácticos?
La fórmula para calcular el área de un rombo es: **Área = (diagonal mayor x diagonal menor) / 2**.
Para aplicar esta fórmula a diferentes ejemplos prácticos, consideremos el siguiente caso:
Ejemplo 1: Supongamos que tenemos un rombo con una diagonal mayor de 8 cm y una diagonal menor de 6 cm. Para calcular el área, podemos utilizar la fórmula que mencionamos anteriormente:
**Área = (8 cm x 6 cm) / 2 = 48 cm²**
Por lo tanto, el área de este rombo sería de 48 cm².
Ejemplo 2: Ahora, imaginemos que tenemos un rombo con una diagonal mayor de 10 metros y una diagonal menor de 7 metros. Aplicando la fórmula del área:
**Área = (10 m x 7 m) / 2 = 35 m²**
En este caso, el área del rombo sería de 35 metros cuadrados.
Estos son solo dos ejemplos prácticos de cómo aplicar la fórmula del área de un rombo en situaciones reales. Recuerda que siempre debes asegurarte de conocer las medidas correctas de las diagonales antes de utilizar la fórmula.
¿Cuáles son las propiedades específicas de un rombo y cómo se pueden utilizar en ejemplos reales para resolver problemas de geometría o física?
El rombo es un tipo de cuadrilátero que tiene algunas propiedades específicas que lo distinguen de otros polígonos. Algunas de estas propiedades son:
1. Lados iguales: En un rombo, los cuatro lados tienen la misma longitud. Esto significa que si conocemos la longitud de uno de los lados, automáticamente conocemos la longitud de los otros tres.
2. Ángulos iguales: Los ángulos opuestos en un rombo son iguales. Esto significa que si conocemos el valor de uno de los ángulos, automáticamente conocemos el valor de los otros tres.
3. Diagonales perpendiculares: Las diagonales de un rombo se intersectan en ángulos rectos, lo que significa que son perpendiculares entre sí.
Estas propiedades del rombo pueden ser utilizadas en ejemplos reales para resolver problemas de geometría o física. A continuación, se presentan dos ejemplos:
Ejemplo 1: Calculando el área de un rombo
Supongamos que tenemos un rombo con un lado de longitud 6 cm y una de sus diagonales de longitud 8 cm. ¿Cuál es su área?
Podemos utilizar la fórmula del área de un rombo, que es “Área = (diagonal1 x diagonal2) / 2”. En este caso, la diagonal1 es 8 cm y la diagonal2 es también 8 cm (ya que las diagonales de un rombo tienen la misma longitud). Sustituyendo estos valores en la fórmula, obtenemos:
Área = (8 cm x 8 cm) / 2 = 64 cm² / 2 = 32 cm²
Por lo tanto, el área del rombo es de 32 cm².
Ejemplo 2: Encontrando la altura de un rombo en un problema físico
Supongamos que tenemos un rombo cuyos lados miden 10 cm y conocemos uno de sus ángulos, que es de 60 grados. Queremos encontrar la altura del rombo (la distancia entre dos lados paralelos).
Podemos utilizar la fórmula de la altura de un rombo, que es “Altura = lado x seno(ángulo)”. En este caso, el lado es 10 cm y el ángulo es de 60 grados. Sustituyendo estos valores en la fórmula, obtenemos:
Altura = 10 cm x sen(60°)
Utilizando una calculadora o tabla de senos, encontramos que el seno de 60 grados es 0.866. Sustituyendo este valor en la fórmula, obtenemos:
Altura = 10 cm x 0.866 = 8.66 cm
Por lo tanto, la altura del rombo es de aproximadamente 8.66 cm.
En resumen, las propiedades específicas del rombo, como los lados iguales, los ángulos iguales y las diagonales perpendiculares, pueden ser utilizadas en ejemplos reales para resolver problemas de geometría o física. Estas propiedades nos permiten calcular áreas, alturas y otros valores relacionados con el rombo.
En conclusión, el estudio y análisis de los Rombo Ejemplos nos permiten comprender las propiedades y características de esta figura geométrica de cuatro lados. A través de ejemplos precisos, hemos observado cómo los rombos son polígonos con lados iguales y ángulos opuestos congruentes. Además, su simetría axial y rotacional los convierte en figuras equilibradas y estéticamente agradables. Estos ejemplos nos muestran la versatilidad de los rombos en diversas situaciones, desde la arquitectura hasta las artes visuales. En resumen, los Rombo Ejemplos son un recurso invaluable para la enseñanza y el aprendizaje de la geometría, brindándonos una visión más profunda y comprensiva de esta fascinante figura geométrica.




















