La frecuencia porcentual es una herramienta fundamental en el análisis de datos, permitiendo visualizar y comprender la distribución de variables en un conjunto de datos. En este artículo, exploraremos ejemplos prácticos que ilustran su aplicación en diversas áreas, como la estadística, la investigación social y el marketing. A través de estos ejemplos, descubrirás cómo calcular e interpretar la frecuencia porcentual de manera efectiva, potenciando tus habilidades analíticas y facilitando la toma de decisiones informadas.
Prepárate para sumergirte en un mundo donde los números cobran vida y revelan historias ocultas.
Contenido
- Explorando Ejemplos de Frecuencia Porcentual en Diferentes Contextos
- Definición de Frecuencia Porcentual
- Ejemplos Prácticos de Frecuencia Porcentual
- Diferencias entre Frecuencia Absoluta y Frecuencia Porcentual
- Interpretación de Resultados en Frecuencia Porcentual
- Limitaciones de la Frecuencia Porcentual
- Preguntas Frecuentes
Explorando Ejemplos de Frecuencia Porcentual en Diferentes Contextos
La frecuencia porcentual es una herramienta estadística que permite expresar la proporción de un evento respecto al total de observaciones, lo cual facilita la comparación y el análisis en diversos contextos. A continuación se presentan ejemplos de frecuencia porcentual en diferentes ámbitos, destacando su relevancia y aplicación.
- Salud Pública: En estudios epidemiológicos, se utiliza la frecuencia porcentual para evaluar la prevalencia de enfermedades. Por ejemplo, si en una población de 1,000 personas, 200 tienen diabetes, la frecuencia porcentual de diabetes sería del 20%. Este dato es crucial para entender el impacto de la enfermedad en la comunidad.
- Educación: En el análisis de resultados académicos, los docentes pueden utilizar la frecuencia porcentual para medir el desempeño de los estudiantes. Si en una clase de 30 alumnos, 24 aprobaron un examen, la frecuencia porcentual de aprobación es del 80%. Esto permite evaluar la efectividad de la enseñanza y realizar ajustes si es necesario.
- Mercadotecnia: Las empresas emplean la frecuencia porcentual para analizar las preferencias de los consumidores. Por ejemplo, en una encuesta de satisfacción, si 150 de 300 encuestados prefieren un producto específico, la frecuencia porcentual de preferencia es del 50%. Este conocimiento guía las decisiones de marketing y desarrollo de productos.
- Investigación Social: En estudios sobre actitudes y comportamientos, la frecuencia porcentual puede servir para entender tendencias. Si en una investigación sobre hábitos de consumo, 80 de 200 participantes indican que compran en línea, la frecuencia porcentual de compra en línea es del 40%. Esta información es valiosa para identificar cambios en el comportamiento del consumidor.
Además de estos ejemplos, podemos observar la aplicación de la frecuencia porcentual en otros contextos:
- Deportes: En el análisis de rendimiento deportivo, se puede calcular la frecuencia porcentual de victorias de un equipo. Si un equipo juega 20 partidos y gana 15, su frecuencia porcentual de victorias es del 75%.
- Ciencias Ambientales: En estudios sobre contaminación, se puede utilizar la frecuencia porcentual para reportar el porcentaje de muestras de agua que exceden límites de contaminantes. Si de 100 muestras, 10 superan los niveles permitidos, la frecuencia porcentual de muestras contaminadas es del 10%.
- Psicología: En investigaciones sobre trastornos psicológicos, la frecuencia porcentual ayuda a determinar la prevalencia de ciertos trastornos en diferentes grupos demográficos. Si en una muestra de 500 personas, 50 son diagnosticadas con ansiedad, la frecuencia porcentual es del 10%.
Estos ejemplos ilustran cómo la frecuencia porcentual es una herramienta versátil y fundamental en el análisis de datos en múltiples disciplinas, facilitando la toma de decisiones informadas y la identificación de patrones significativos. Su capacidad para simplificar información compleja la convierte en un recurso esencial en la investigación y la práctica profesional.
Definición de Frecuencia Porcentual
Concepto Básico
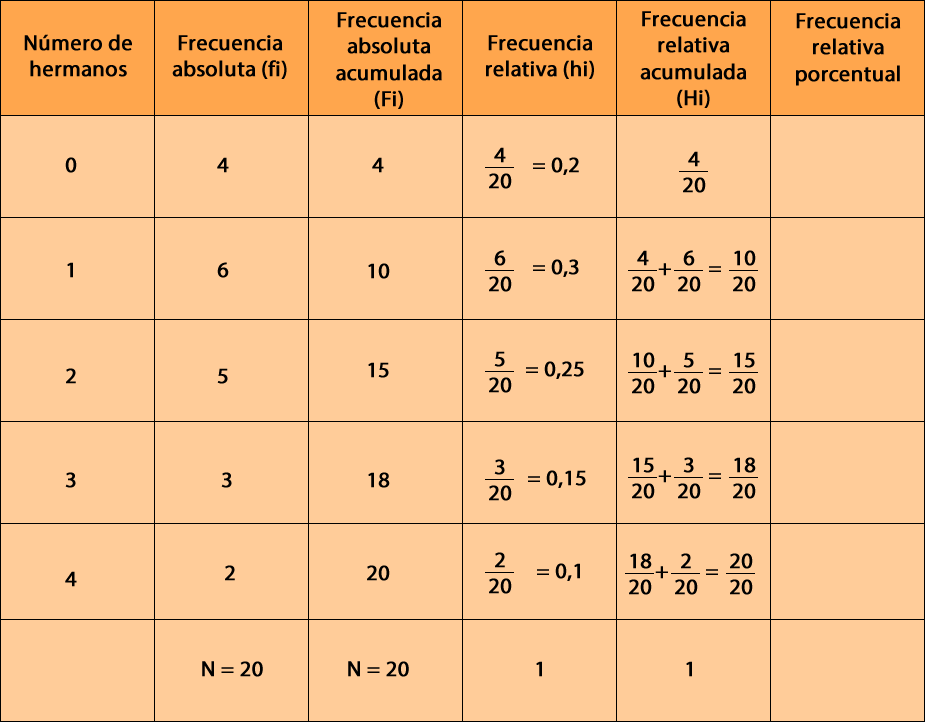
La frecuencia porcentual es una medida que permite expresar la proporción de un conjunto de datos en relación con el total. Se calcula dividiendo la frecuencia absoluta de un evento entre el total de observaciones y multiplicando el resultado por 100. Este concepto es fundamental en estadística, ya que facilita la comprensión de cómo se distribuyen los datos en un estudio.
Fórmula de Cálculo
Para calcular la frecuencia porcentual, utilizamos la siguiente fórmula:
- Frecuencia Absoluta (FA)
- Total de Observaciones (N)
- Frecuencia Porcentual (FP) = (FA / N) * 100
Por ejemplo, si en un estudio de preferencias de frutas, 30 personas eligen manzana de un total de 100 encuestados, la frecuencia porcentual de la manzana sería (30/100) * 100 = 30%.
Ejemplos Prácticos de Frecuencia Porcentual
Aplicación en Encuestas
Las encuestas son uno de los contextos más comunes donde se aplica la frecuencia porcentual. Al realizar una encuesta sobre hábitos de consumo, se puede querer saber qué porcentaje de la población prefiere un tipo de producto. Supongamos que en una encuesta sobre bebidas, 50 personas prefieren el té, 30 el café y 20 el agua.
Calculando la frecuencia porcentual para cada opción tenemos:
- Té: (50/100) * 100 = 50%
- Café: (30/100) * 100 = 30%
- Agua: (20/100) * 100 = 20%
Estos resultados permiten a las empresas tomar decisiones informadas sobre su oferta de productos.
Uso en Reportes Estadísticos
En los informes estadísticos, la frecuencia porcentual se utiliza para resumir y presentar resultados de manera clara. Por ejemplo, un análisis demográfico puede incluir tablas que muestren la distribución de edades en porcentajes. Esto no solo facilita la interpretación de los datos, sino que también permite comparaciones rápidas entre diferentes grupos.
Un ejemplo podría ser un reporte que indique que el 25% de la población está en el grupo de edad de 18-25 años, el 35% en 26-35 años, y así sucesivamente. Este formato ayuda a visualizar la composición de la población de forma efectiva.
Diferencias entre Frecuencia Absoluta y Frecuencia Porcentual
Conceptos Distintos
La frecuencia absoluta se refiere al número total de veces que ocurre un evento en un conjunto de datos. En contraste, la frecuencia porcentual muestra esa misma información como un porcentaje del total. Así, aunque ambas frecuencias ofrecen información valiosa, cada una lo hace desde distintas perspectivas.
Por ejemplo, si en un conjunto de datos de 200 respuestas, 40 personas eligieron una opción, la frecuencia absoluta es 40, mientras que la frecuencia porcentual sería (40/200) * 100 = 20%. Esto resalta la importancia de ambos conceptos en la interpretación de datos.
Importancia en el Análisis de Datos
Entender la diferencia entre frecuencia absoluta y frecuencia porcentual es crucial para el análisis de datos. La frecuencia absoluta puede ser útil para determinar el volumen total de respuestas, mientras que la frecuencia porcentual ayuda a interpretar esos datos en el contexto de tamaño total de la muestra.
Usar ambas medidas en conjunto puede proporcionar una visión más completa de los resultados. Por ejemplo, en un estudio de satisfacción del cliente, una alta frecuencia absoluta en respuestas negativas puede ser menos preocupante si el número total de encuestas es muy bajo.
Interpretación de Resultados en Frecuencia Porcentual
Análisis Crítico de los Datos
La interpretación de los resultados de frecuencia porcentual requiere un análisis crítico. No basta con conocer los porcentajes; es fundamental entender el contexto de los datos. Por ejemplo, si un 70% de los encuestados reporta estar satisfechos, ¿qué significa esto en términos de calidad del servicio?
Es importante considerar factores como el tamaño de la muestra, el método de recolección de datos y posibles sesgos en la muestra. Una alta frecuencia porcentual puede ser engañosa si no se analizan estos aspectos.
Visualización de Resultados
Para facilitar la comprensión de los datos, es recomendable utilizar gráficos que representen visualmente las frecuencias porcentuales. Gráficos de barras o pasteles son herramientas efectivas para mostrar cómo se distribuyen los datos entre las diferentes categorías.
Por ejemplo, un gráfico circular que represente las preferencias de un producto puede hacer que sea más fácil para los tomadores de decisiones identificar qué opciones son más populares, lo que a su vez puede influir en la estrategia de marketing.
Limitaciones de la Frecuencia Porcentual
Posibles Sesgos en la Muestra
Uno de los principales problemas al utilizar frecuencias porcentuales es el riesgo de sesgo en la muestra. Si la muestra no es representativa de la población, los resultados pueden llevar a conclusiones erróneas. Por ejemplo, si solo se encuesta a un grupo específico, los porcentajes obtenidos no reflejarán necesariamente la realidad del total de la población.
Contexto de Interpretación
Además, es crucial tener en cuenta que la frecuencia porcentual no proporciona información sobre la magnitud del fenómeno. Un 10% puede parecer bajo en un contexto, pero significativo en otro. Por lo tanto, siempre es recomendable analizar los datos en su totalidad, incluyendo la frecuencia absoluta y el contexto en el que se han recolectado los mismos.
Con este enfoque integral, se puede obtener una comprensión más completa y precisa de los datos analizados.
Preguntas Frecuentes
¿Cuáles son los pasos para calcular la frecuencia porcentual a partir de un conjunto de datos?
Para calcular la frecuencia porcentual a partir de un conjunto de datos, sigue estos pasos:
1. Cuenta el número de veces que ocurre cada categoría en el conjunto de datos.
2. Suma todas las frecuencias para obtener el total de observaciones.
3. Para cada categoría, divide la frecuencia de la categoría entre el total de observaciones.
4. Multiplica el resultado por 100 para obtener el porcentaje.
Esto te dará la frecuencia porcentual de cada categoría.
¿Qué ejemplos ilustran la aplicación de la frecuencia porcentual en investigaciones estadísticas?
En investigaciones estadísticas, la frecuencia porcentual se utiliza para resumir datos de diversas maneras. Por ejemplo:
1. En una encuesta sobre hábitos de consumo, se puede reportar que el 60% de los encuestados prefieren comprar en línea.
2. En un estudio educativo, se podría indicar que el 75% de los estudiantes aprobaron el examen final.
3. En una investigación de mercado, se puede encontrar que el 40% de los participantes utilizan redes sociales diariamente.
Estos ejemplos muestran cómo la frecuencia porcentual ayuda a interpretar y comunicar resultados de manera efectiva.
¿Cómo se interpreta la frecuencia porcentual en el contexto de un análisis de datos?
La frecuencia porcentual en un análisis de datos se interpreta como la proporción de un grupo específico en relación con el total, expresada en porcentaje. Por ejemplo, si en una encuesta el 40% de los encuestados prefiere el producto A, esto indica que de cada 100 personas, 40 eligen el producto A. Esta medida permite comparar y entender tendencias dentro de los datos analizados.
¿Qué diferencias existen entre la frecuencia absoluta y la frecuencia porcentual en la presentación de resultados?
La frecuencia absoluta se refiere al número total de veces que ocurre un evento en un conjunto de datos, mientras que la frecuencia porcentual muestra el porcentaje que representa esa frecuencia absoluta respecto al total de observaciones. Por ejemplo, si en una encuesta 20 personas prefieren el café y el total de encuestados es 100, la frecuencia absoluta es 20 y la frecuencia porcentual es 20%.
En conclusión, los ejemplos de frecuencia porcentual son fundamentales para una adecuada comprensión de datos en diversas disciplinas. Su aplicación permite un análisis más efectivo y claro. Te invitamos a compartir este contenido y a seguir explorando más sobre estadísticas y su importancia en la investigación. ¡Tu participación es valiosa!