¿Te has preguntado alguna vez cómo las funciones se interrelacionan entre sí? Los diagramas de Venn son herramientas visuales que nos permiten explorar estas conexiones de manera clara y efectiva. En este artículo, analizaremos ejemplos concretos que ilustran cómo se pueden representar diferentes conjuntos y sus intersecciones utilizando estas diagramas.
Acompáñanos en este recorrido académico donde desglosaremos sus aplicaciones y te proporcionaremos las claves para comprender mejor esta fascinante área de la matemática.
Contenido
Ejemplos Prácticos de Diagramas de Venn: Comprendiendo Funciones y Relaciones
Los diagramas de Venn son herramientas visuales poderosas que permiten representar relaciones y funciones entre diferentes conjuntos. Su utilidad se extiende a campos como la matemática, la estadística, la lógica y la ciencia de datos. A continuación, se presentan algunos ejemplos prácticos que ilustran cómo se pueden aplicar estos diagramas en diversas situaciones.
- Comparación de Grupos: Supongamos que tenemos dos grupos de estudiantes: uno que estudia matemáticas y otro que estudia ciencias. Un diagrama de Venn puede mostrar:
- Los estudiantes que solo estudian matemáticas.
- Los estudiantes que solo estudian ciencias.
- Los estudiantes que estudian ambas materias.
- Análisis de Preferencias: En un estudio de mercado, podemos usar un diagrama de Venn para analizar las preferencias de los consumidores entre tres marcas de un producto. El diagrama mostrará:
- Los consumidores que prefieren la marca A.
- Los consumidores que prefieren la marca B.
- Los consumidores que prefieren la marca C.
- Los consumidores que prefieren combinaciones de marcas (A y B, B y C, etc.).
- Identificación de Elementos Comunes: En biología, se pueden utilizar diagramas de Venn para comparar características de diferentes especies. Por ejemplo, al comparar mamíferos, aves y reptiles, el diagrama puede resaltar:
- Características únicas de cada grupo.
- Características compartidas entre mamíferos y aves (como la capacidad de volar en algunas especies).
- Características comunes a todos los grupos (como la presencia de células con núcleo).
- Estadísticas de Salud: En estudios epidemiológicos, un diagrama de Venn puede ayudar a comprender la relación entre distintos factores de riesgo para una enfermedad. Por ejemplo:
- Fumadores.
- Personas con antecedentes familiares de la enfermedad.
- Individuos con hábitos alimenticios poco saludables.
- La intersección podría mostrar aquellos que tienen múltiples factores de riesgo.
Además, los diagramas de Venn no solo sirven para visualizar y comparar conjuntos, sino que también pueden ser utilizados para resolver problemas lógicos. Por ejemplo, en una situación donde se requiere determinar qué elementos son únicos o comunes entre varios conjuntos, estos diagramas se convierten en una herramienta práctica y efectiva.
En resumen, los diagramas de Venn son una herramienta versátil que facilita la comprensión de funciones y relaciones entre conjuntos diversos. Su capacidad para representar visualmente intersecciones y diferencias los convierte en una opción ideal para una amplia gama de aplicaciones académicas y profesionales.
Introducción a los Diagramas de Venn
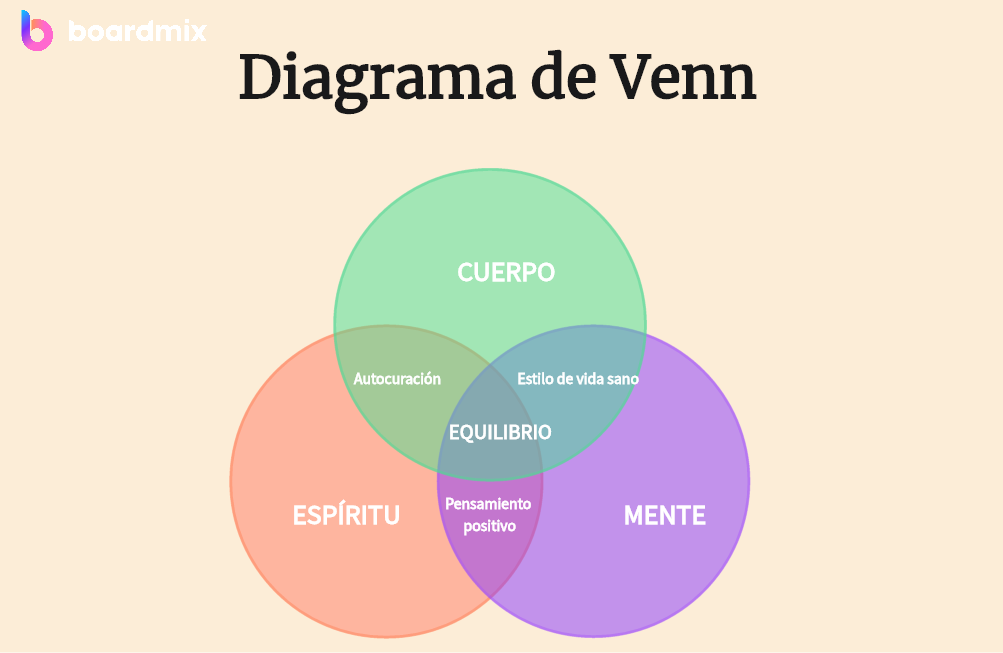
Los Diagramas de Venn son representaciones gráficas que ilustran la relación entre diferentes conjuntos. Su uso es fundamental en diversas áreas del conocimiento, incluyendo matemáticas, lógica y estadísticas. Se componen de círculos que se superponen, cada uno representando un conjunto diferente. La intersección de estos círculos muestra los elementos que comparten los conjuntos.
Características Principales
Los Diagramas de Venn poseen varias características que los hacen únicos y útiles:
- Visualización clara: Permiten visualizar de manera intuitiva la relación y las intersecciones entre conjuntos.
- Simplicidad: Con una representación gráfica sencilla, pueden ser utilizados para explicar conceptos complejos.
- Flexibilidad: Pueden representar dos o más conjuntos, lo que los hace adaptables a diferentes situaciones.
En términos generales, los Diagramas de Venn son herramientas poderosas para la enseñanza y el aprendizaje, facilitando la comprensión de relaciones lógicas y matemáticas.
Ejemplos Prácticos de Diagramas de Venn
Existen múltiples ejemplos prácticos donde los Diagramas de Venn pueden ser aplicados. Estos ejemplos abarcan desde problemas matemáticos hasta situaciones cotidianas. A continuación, se presentan algunos casos que ilustran su uso.
Ejemplo 1: Intersección de Aficiones
Supongamos que tenemos dos conjuntos: el conjunto A representa a las personas que disfrutan de la lectura y el conjunto B representa a aquellas que disfrutan del cine. El Diagrama de Venn en este caso mostraría:
- El círculo A contendría a todos los lectores.
- El círculo B incluiría a los cinéfilos.
- La intersección mostraría a aquellos que disfrutan tanto de leer como de ver películas.
Este ejemplo es útil para entender cómo las preferencias pueden solaparse y resaltar la importancia de considerar las similitudes entre diferentes grupos de personas.
Ejemplo 2: Clasificación de Animales
Otro ejemplo podría ser la clasificación de animales en función de sus características. Por ejemplo, podemos tener el conjunto C que representa a los mamíferos y el conjunto D que representa a los animales que vuelan.
- El círculo C incluiría a todos los mamíferos, como perros y gatos.
- El círculo D incluiría aves como halcones y murciélagos.
- La intersección mostraría a los murciélagos, que son mamíferos que también tienen la capacidad de volar.
Este ejemplo demuestra cómo los Diagramas de Venn pueden ser utilizados para clasificar y entender las relaciones entre diferentes categorías biológicas.
Aplicaciones en el Ámbito Educativo
Los Diagramas de Venn son ampliamente utilizados en el ámbito educativo debido a su capacidad para simplificar conceptos complejos. A continuación, se discuten algunas de sus aplicaciones más relevantes.
Facilitación del Aprendizaje
Los Diagramas de Venn facilitan el aprendizaje al permitir que los estudiantes visualicen la información de forma clara. Esto es especialmente útil en materias como matemáticas y ciencias, donde los conceptos abstractos pueden ser difíciles de entender.
- Ayudan a los estudiantes a identificar similitudes y diferencias entre conceptos.
- Fomentan la discusión y el análisis crítico entre compañeros.
- Son herramientas efectivas para preparar exámenes y trabajos de investigación.
Al utilizar Diagramas de Venn, los educadores pueden mejorar la comprensión de los estudiantes y promover un aprendizaje más interactivo.
Desarrollo de Habilidades de Pensamiento Crítico
Además de facilitar el aprendizaje, los Diagramas de Venn contribuyen al desarrollo de habilidades de pensamiento crítico. Al comparar y contrastar diferentes elementos, los estudiantes aprenden a evaluar información de manera más efectiva.
Esto incluye:
- Analizar datos y reconocer patrones.
- Formular preguntas relevantes sobre la información presentada.
- Desarrollar argumentos basados en evidencia visual.
Estas habilidades son fundamentales no solo en el entorno académico, sino también en la vida cotidiana y profesional.
Limitaciones de los Diagramas de Venn
A pesar de su eficacia, los Diagramas de Venn tienen ciertas limitaciones que deben considerarse al utilizarlos.
Dificultades en Conjuntos Complejos
Cuando se trata de más de tres conjuntos, los Diagramas de Venn pueden volverse confusos. Las intersecciones múltiples pueden dificultar la visualización clara de las relaciones entre los conjuntos.
- Es posible que algunos elementos queden ocultos en el gráfico.
- Puede ser difícil representar visualmente todas las interacciones entre los conjuntos.
- Los diagramas con muchos conjuntos pueden perder su efectividad como herramienta educativa.
Por lo tanto, es importante utilizar Diagramas de Venn con prudencia en situaciones donde la complejidad puede superar su capacidad de representación.
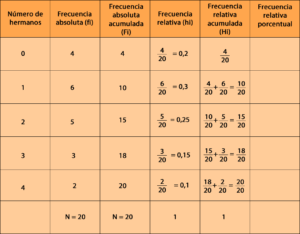
No Siempre Representan Relaciones Cuantitativas
Otra limitación es que los Diagramas de Venn no están diseñados para mostrar relaciones cuantitativas. Aunque pueden ilustrar la existencia de relaciones, no proporcionan datos específicos sobre la cantidad de elementos en cada conjunto.
Esto significa que:
- No se pueden extraer conclusiones numéricas precisas.
- No representan la magnitud de las intersecciones.
- Pueden llevar a malentendidos si se utilizan incorrectamente para inferir cantidades.
Como resultado, es crucial complementar el uso de Diagramas de Venn con otros métodos de análisis cuando sea necesario obtener información cuantitativa.
Preguntas Frecuentes
¿Cuáles son las principales características de un diagrama de Venn en la representación de funciones matemáticas?
Un diagrama de Venn en la representación de funciones matemáticas se caracteriza por:
1. Conjuntos: Representa conjuntos de elementos que pueden ser iguales o diferentes.
2. Intersección: Muestra la intersección de conjuntos, indicando elementos comunes.
3. Unión: Permite visualizar la unión de conjuntos, que incluye todos los elementos de ambos.
4. Complemento: Ayuda a identificar el complemento de un conjunto, es decir, lo que no pertenece a él.
Estos elementos son esenciales para entender relaciones entre funciones y sus dominios.
¿Cómo se pueden utilizar los diagramas de Venn para ilustrar la intersección y la unión de funciones?
Los diagramas de Venn son útiles para visualizar la intersección y la unión de funciones al representar conjuntos. Por ejemplo, si tenemos dos funciones A y B, la intersección (A ∩ B) se muestra como la zona compartida entre los círculos que representan A y B, indicando los valores comunes. La unión (A ∪ B) abarca toda el área cubierta por ambos círculos, mostrando todos los valores de A y B juntos. Esto ayuda a entender cómo se relacionan las funciones en términos de sus resultados.
¿Qué ejemplos prácticos existen de la aplicación de diagramas de Venn en el análisis de funciones?
Los diagramas de Venn se utilizan en el análisis de funciones para visualizar relaciones entre conjuntos. Por ejemplo, al analizar la intersección de dos funciones, se puede usar un diagrama de Venn para mostrar los valores que comparten. Otro ejemplo es en la unión de funciones, donde se representan todos los valores posibles de ambas funciones. También son útiles para identificar valores excluidos, ayudando a comprender mejor el dominio y rango de cada función.
¿Qué limitaciones presentan los diagramas de Venn al representar funciones complejas?
Los diagramas de Venn presentan limitaciones significativas al representar funciones complejas debido a que son más adecuados para mostrar relaciones simples entre conjuntos. No pueden capturar interacciones múltiples o dependencias complejas entre variables, lo que los hace insuficientes para ilustrar funciones matemáticas avanzadas o situaciones con múltiples dimensiones. Además, su visualización puede volverse confusa cuando se incluyen muchos conjuntos, lo que dificulta la interpretación.
En conclusión, los diagramas de Venn son herramientas visuales fundamentales para comprender las funciones y relaciones entre conjuntos. A través de diversos ejemplos, hemos explorado su aplicabilidad en distintos contextos. Te invitamos a compartir este contenido y seguir leyendo más sobre temas relacionados.