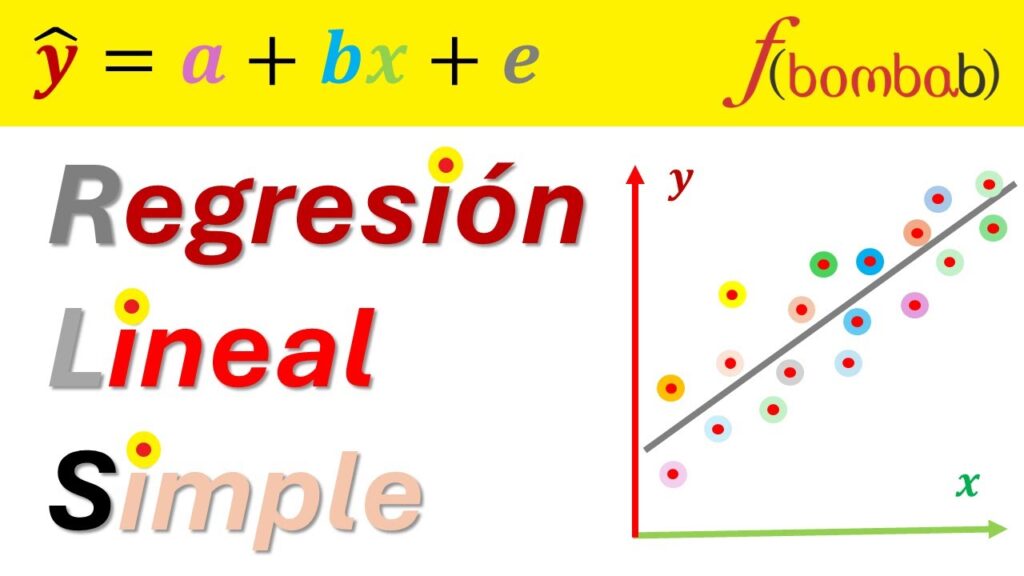
La regresión lineal simple es una herramienta fundamental en el análisis de datos, utilizada para comprender la relación entre dos variables cuantitativas. A través de este artículo, exploraremos diversos ejemplos prácticos que ilustran cómo aplicar este método en situaciones reales, desde el ámbito económico hasta el social.
Si deseas profundizar en cómo la regresión lineal puede ayudarte a interpretar tus datos y realizar predicciones efectivas, sigue leyendo para descubrir las aplicaciones y beneficios de esta técnica estadística.
Contenido
Ejemplos Prácticos de Regresión Lineal Simple: Aplicaciones en el Mundo Real
La regresión lineal simple es una técnica estadística que permite modelar la relación entre dos variables, donde una de ellas se considera dependiente y la otra independiente. A continuación, se presentan varios ejemplos prácticos de su aplicación en el mundo real.
- Predicción de ventas: Las empresas pueden utilizar la regresión lineal simple para prever sus ventas en función de factores como el gasto en publicidad. Por ejemplo, un análisis puede mostrar que por cada aumento de $1,000 en la inversión publicitaria, las ventas aumentan en $5,000.
- Estudio de la relación entre temperatura y consumo de energía: Las compañías de energía a menudo emplean la regresión lineal simple para entender cómo la temperatura afecta el consumo energético. En este caso, la temperatura sería la variable independiente y el consumo de energía la variable dependiente.
- Análisis de precios de vivienda: La regresión lineal simple se utiliza en el sector inmobiliario para analizar cómo diferentes características de una vivienda, como el tamaño o la ubicación, influyen en su precio. Por ejemplo, se podría establecer que cada metro cuadrado adicional aumenta el precio en $200.
- Estudios en salud pública: En el ámbito de la salud, se pueden utilizar modelos de regresión lineal simple para investigar la relación entre el índice de masa corporal (IMC) y la presión arterial. Esto puede ayudar a identificar tendencias entre estas variables.
Además de estos ejemplos, hay muchas otras aplicaciones que demuestran la utilidad de la regresión lineal simple:
- Estudios de mercado: Se pueden realizar encuestas para determinar cómo la satisfacción del cliente se relaciona con el número de quejas recibidas.
- Investigación educativa: Se puede analizar la relación entre las horas de estudio y el rendimiento académico de los estudiantes.
- Economía: Los economistas utilizan la regresión lineal simple para estudiar la relación entre el ingreso y el gasto de los hogares.
- Ecología: En estudios ambientales, se pueden analizar los efectos de la contaminación en la biodiversidad de una región mediante la regresión lineal.
La implementación de la regresión lineal simple en estos contextos demuestra su versatilidad y efectividad como herramienta analítica. A través de la identificación y cuantificación de relaciones entre variables, permite a investigadores y profesionales tomar decisiones informadas basadas en datos. Además, su simplicidad en la interpretación facilita su uso en diversas disciplinas, lo que la convierte en un recurso valioso en el análisis cuantitativo.
Definición y Fundamentos de la Regresión Lineal Simple
La regresión lineal simple es una técnica estadística utilizada para modelar la relación entre dos variables cuantitativas, donde una variable se considera dependiente y la otra independiente. El objetivo principal es encontrar la línea de mejor ajuste que minimice la suma de los cuadrados de las diferencias entre los valores observados y los valores predichos por el modelo.
Concepto de Variables
En el contexto de la regresión lineal simple, es fundamental entender el rol de las variables. La variable dependiente es aquella que se desea predecir o explicar, mientras que la variable independiente es la que se manipula o se utiliza como predictor. Por ejemplo, si se está analizando cómo afecta el número de horas de estudio (variable independiente) en el rendimiento académico (variable dependiente), se busca establecer una relación que permita prever el rendimiento basado en las horas de estudio.
- Variable Dependiente: Resultados académicos.
- Variable Independiente: Horas de estudio.
Ecuación de la Recta de Regresión
La relación entre las variables se puede expresar mediante la ecuación de la recta de regresión:
Y = a + bX
donde:
- Y es la variable dependiente.
- X es la variable independiente.
- a es la intersección en el eje Y (valor cuando X=0).
- b es la pendiente de la línea (cambio en Y por cada unidad de cambio en X).
Esta ecuación permite hacer predicciones sobre la variable dependiente basándose en los valores de la variable independiente.
Ejemplo Práctico de Regresión Lineal Simple
Para ilustrar la aplicación de la regresión lineal simple, consideremos el siguiente ejemplo práctico: un investigador desea determinar cómo el ingreso familiar (en miles de pesos) influye en el gasto en educación de los hogares (en miles de pesos).
Recolección de Datos
El primer paso en este tipo de análisis es la recolección de datos. En este caso, el investigador podría realizar encuestas a varias familias, recopilando información sobre su ingreso y el gasto destinado a la educación. Por ejemplo, se podrían obtener datos de 10 hogares con los siguientes ingresos y gastos:
- Ingreso: 30, Gasto: 5
- Ingreso: 40, Gasto: 8
- Ingreso: 50, Gasto: 12
- Ingreso: 60, Gasto: 15
- Ingreso: 70, Gasto: 18
- Ingreso: 80, Gasto: 20
- Ingreso: 90, Gasto: 25
- Ingreso: 100, Gasto: 28
- Ingreso: 110, Gasto: 30
- Ingreso: 120, Gasto: 35
Aplicación del Modelo
Una vez recolectados los datos, se procede a aplicar el modelo de regresión lineal. Utilizando software estadístico, se pueden calcular los parámetros ‘a’ y ‘b’. Supongamos que, tras el análisis, se obtienen:
a = -2 y b = 0.3.
Esto significa que la ecuación de regresión sería:
Gasto = -2 + 0.3 * Ingreso
Esta fórmula indica que, por cada mil pesos de incremento en el ingreso familiar, se espera que el gasto en educación aumente en aproximadamente 300 pesos.
Interpretación de Resultados
La interpretación de los resultados obtenidos es crucial para la toma de decisiones informadas basadas en el modelo de regresión.
Significado de los Coeficientes
Los coeficientes ‘a’ y ‘b’ tienen un significado importante. En este caso, el valor negativo de ‘a’ sugiere que, si no hubiera ingreso, el gasto en educación sería negativo, lo cual no tiene sentido práctico, pero es parte del modelo matemático. Por otro lado, la pendiente ‘b’ indica que existe una relación positiva entre el ingreso y el gasto en educación.
Evaluación del Modelo
Para evaluar la efectividad del modelo, se pueden utilizar métricas como el coeficiente de determinación (R²), que indica la proporción de la varianza de la variable dependiente que es explicada por la variable independiente. Un R² cercano a 1 indica que el modelo explica bien la variabilidad de los datos.
Limitaciones de la Regresión Lineal Simple
A pesar de su utilidad, la regresión lineal simple tiene limitaciones que deben ser consideradas.
Suposiciones del Modelo
El modelo de regresión lineal simple se basa en varias suposiciones, tales como la linealidad, homocedasticidad y normalidad de los errores. Si estas condiciones no se cumplen, los resultados pueden ser engañosos. Es fundamental verificar estas suposiciones antes de confiar plenamente en los resultados del modelo.
Relaciones No Lineales
Además, la regresión lineal simple solo es adecuada para relaciones lineales. Si la relación entre las variables es no lineal, el modelo podría no ser el más adecuado. En tales casos, se podría considerar la regresión polinómica u otras técnicas más complejas.
Conclusiones y Aplicaciones Futuras
La regresión lineal simple es una herramienta poderosa en la investigación y análisis de datos. Su capacidad para modelar relaciones entre variables permite a los investigadores obtener información valiosa.
Importancia en la Toma de Decisiones
Los resultados derivados de este tipo de análisis pueden influir en la toma de decisiones en diversas áreas, como economía, educación y salud. Las predicciones basadas en modelos de regresión pueden ayudar a formular políticas y estrategias efectivas.
Perspectivas de Investigación Futura
Futuras investigaciones podrían ampliar la comprensión de las relaciones complejas entre múltiples variables utilizando la regresión múltiple, lo cual permitiría explorar interacciones y efectos combinados en mayor profundidad.
Preguntas Frecuentes
¿Cuáles son algunos ejemplos prácticos de regresión lineal simple en estudios económicos?
Algunos ejemplos prácticos de regresión lineal simple en estudios económicos incluyen:
1. Relación entre ingresos y consumo: Analizar cómo el aumento en los ingresos de los hogares afecta su gasto en bienes.
2. Impacto del salario mínimo: Estudiar la relación entre el salario mínimo y la tasa de empleo en una región.
3. Demanda de productos: Evaluar cómo el precio de un producto influye en su demanda.
Estos ejemplos ayudan a comprender mejor las dinámicas económicas mediante la modelización de variables.
¿Cómo se aplica la regresión lineal simple en la predicción de ventas a partir de variables independientes?
La regresión lineal simple se aplica en la predicción de ventas analizando la relación entre una variable independiente (como el gasto en publicidad) y la variable dependiente (ventas). Por ejemplo, al recopilar datos sobre el gasto publicitario y las ventas realizadas, se puede crear un modelo que permita estimar las ventas futuras basándose en nuevos niveles de inversión en publicidad. Este análisis ayuda a las empresas a optimizar recursos y mejorar estrategias de marketing.
¿Qué ejemplos ilustran el uso de la regresión lineal simple en investigaciones científicas?
La regresión lineal simple se utiliza en diversas investigaciones científicas. Por ejemplo, en estudios de salud pública, se puede analizar la relación entre el consumo de tabaco y la incidencia de cáncer de pulmón. También se aplica en ecología para evaluar cómo la temperatura afecta el crecimiento de plantas. En economía, se puede examinar la relación entre el ingreso per cápita y el nivel de educación en una población. Estos ejemplos muestran cómo la regresión lineal simple ayuda a identificar patrones y relaciones entre variables.
¿De qué manera la regresión lineal simple se utiliza para analizar la relación entre el tiempo de estudio y el rendimiento académico?
La regresión lineal simple se utiliza para analizar la relación entre el tiempo de estudio y el rendimiento académico al modelar cómo varía el rendimiento en función del tiempo dedicado al estudio. Por ejemplo, si se recopilan datos sobre horas de estudio y calificaciones, se puede trazar una línea que indique la tendencia general: a mayor tiempo de estudio, mejor rendimiento académico. Esto permite predecir el rendimiento basado en el tiempo de estudio invertido.
En conclusión, la regresión lineal simple se presenta como una herramienta fundamental en el análisis de datos. Sus aplicaciones prácticas, ejemplificadas en este artículo, evidencian su relevancia en diversas disciplinas. Te invitamos a compartir este contenido y a seguir explorando más sobre este fascinante tema. ¡Tu aprendizaje continúa!