¿Alguna vez te has preguntado cómo visualizar una función matemática de manera efectiva? La imagen de una función es un concepto fundamental que permite comprender las relaciones entre variables y sus comportamientos. En este artículo, exploraremos diversos ejemplos que ilustran cómo se determina la imagen de diferentes funciones, facilitando así el análisis gráfico y analítico.
Acompáñanos en este recorrido y descubre el impacto que tiene la representación visual en el estudio de las matemáticas. ¡Sigue leyendo para desentrañar este fascinante tema!
Contenido
Ejemplos Ilustrativos de Imágenes de Funciones: Comprendiendo Conceptos Clave
Los ejemplos ilustrativos de imágenes de funciones son herramientas fundamentales para comprender conceptos clave en matemáticas, particularmente en el estudio de funciones. Las funciones son relaciones entre un conjunto de entradas (dominio) y un conjunto de salidas (codominio), y su representación gráfica permite visualizar cómo se comportan. A continuación, se presentan algunos ejemplos que facilitan la comprensión de este tema.
1. Función Lineal: Una función lineal puede expresarse como ( f(x) = mx + b ), donde ( m ) es la pendiente y ( b ) es el punto donde la línea corta al eje ( y ). La representación gráfica de esta función es una línea recta. Para ilustrar esto:
- Si ( m = 2 ) y ( b = 1 ), la función será ( f(x) = 2x + 1 ).
- Los puntos de la función son: ( (0, 1) ), ( (1, 3) ), y ( (2, 5) ).
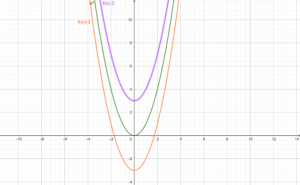
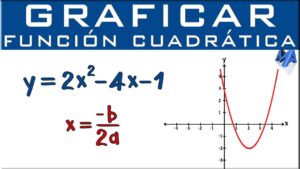
2. Función Cuadrática: Una función cuadrática tiene la forma ( f(x) = ax^2 + bx + c ). Su representación gráfica es una parábola. Por ejemplo:
- Si ( a = 1 ), ( b = 0 ) y ( c = 0 ), la función será ( f(x) = x^2 ).
- Los puntos relevantes incluyen: ( (0, 0) ), ( (1, 1) ), y ( (-1, 1) ).
3. Función Exponencial: Las funciones exponenciales son de la forma ( f(x) = a cdot b^x ), donde ( a ) es un coeficiente y ( b ) es la base de la potencia. Un caso común es:
- Para ( a = 1 ) y ( b = 2 ), la función resultante es ( f(x) = 2^x ).
- Algunos puntos notables son: ( (0, 1) ), ( (1, 2) ), y ( (2, 4) ).
4. Función Logarítmica: Esta función es la inversa de la función exponencial y se expresa como ( f(x) = log_b(x) ). Un ejemplo sería:
- Si ( b = 10 ), entonces ( f(x) = log_{10}(x) ).
- Los puntos importantes incluyen: ( (1, 0) ), ( (10, 1) ), y ( (100, 2) ).
5. Función Trigonométrica: Las funciones trigonométricas, como el seno y el coseno, son fundamentales en el análisis de fenómenos periódicos. Por ejemplo:
- La función seno se representa como ( f(x) = sin(x) ).
- Algunos puntos destacados son: ( (0, 0) ), ( (frac{pi}{2}, 1) ), y ( (pi, 0) ).
La representación gráfica de estas funciones no solo ayuda a entender sus propiedades sino que también permite identificar características como la continuidad, la periodicidad y los extremos. Además, estas imágenes son cruciales en aplicaciones prácticas, desde la ingeniería hasta las ciencias sociales, donde el comportamiento de diversas variables debe analizarse y preverse.
Definición de imagen de una función
Concepto básico
La imagen de una función se refiere al conjunto de todos los valores que la función puede tomar. En términos matemáticos, si tenemos una función ( f: A rightarrow B ), donde ( A ) es el dominio y ( B ) es el codominio, la imagen de la función es el subconjunto de ( B ) que se obtiene al aplicar ( f ) a cada elemento de ( A ).
Ejemplo práctico
Consideremos la función cuadrática ( f(x) = x^2 ). Si nuestro dominio es ( A = {-2, -1, 0, 1, 2} ), la imagen de esta función sería:
- Para ( x = -2 ), ( f(-2) = 4 )
- Para ( x = -1 ), ( f(-1) = 1 )
- Para ( x = 0 ), ( f(0) = 0 )
- Para ( x = 1 ), ( f(1) = 1 )
- Para ( x = 2 ), ( f(2) = 4 )
Así, la imagen de la función sería ( {0, 1, 4} ).
Propiedades de la imagen de una función
Inyectividad y sobreyectividad
Las propiedades de inyectividad y sobreyectividad son fundamentales para comprender la imagen de una función.
- Una función es inyectiva si diferentes elementos del dominio tienen imágenes diferentes.
- Una función es sobreyectiva si su imagen coincide con todo el codominio.
Por ejemplo, la función ( f(x) = 2x ) es inyectiva porque no hay dos valores diferentes de ( x ) que produzcan el mismo resultado. Sin embargo, si consideramos la función ( g(x) = x^2 ), no es inyectiva porque tanto ( g(1) ) como ( g(-1) ) dan como resultado ( 1 ).
Importancia en la matemática
Entender la imagen de una función es crucial en múltiples áreas de las matemáticas, incluyendo el cálculo y la teoría de conjuntos. La imagen nos permite identificar cómo se comporta una función dentro de un contexto particular y es fundamental para el estudio de límites y continuidad.
Además, la imagen de una función puede ayudar a resolver ecuaciones algebraicas y a encontrar raíces, ya que conocer los posibles valores de salida facilita la identificación de soluciones.
Ejemplos de funciones y sus imágenes
Función lineal
Consideremos la función lineal ( h(x) = 3x + 2 ). Si tomamos un dominio ( D = {0, 1, 2, 3} ), podemos calcular la imagen:
- Para ( x = 0 ), ( h(0) = 2 )
- Para ( x = 1 ), ( h(1) = 5 )
- Para ( x = 2 ), ( h(2) = 8 )
- Para ( x = 3 ), ( h(3) = 11 )
Por lo tanto, la imagen de la función lineal sería ( {2, 5, 8, 11} ).
Función trigonométrica
Analicemos ahora la función ( k(x) = sin(x) ) en el intervalo ( [0, 2pi] ). La imagen de esta función abarca todos los valores desde ( -1 ) hasta ( 1 ). Es decir, aunque el dominio sea restringido, la imagen cubre un rango completo de valores.
Esto es un buen ejemplo de cómo el comportamiento de la función puede variar dependiendo de su tipo, mostrando que no todas las funciones tienen imágenes discretas.
Aplicaciones de la imagen de una función
En la resolución de problemas
La imagen de una función tiene aplicaciones prácticas en diversas áreas, como la ingeniería y la economía. Por ejemplo, en problemas de optimización, conocer la imagen puede facilitar la identificación de máximos y mínimos. Esto es crucial en campos como la física, donde se busca maximizar la eficiencia de un sistema.
En la programación y las ciencias de la computación
En el ámbito de la programación, entender la imagen de una función puede ser útil para desarrollar algoritmos eficientes. Por ejemplo, en estructuras de datos como árboles y grafos, saber qué valores pueden ser alcanzados por una función ayuda a optimizar búsquedas y recorridos.
Por tanto, la imagen de una función no solo es un concepto teórico, sino que tiene profundas implicaciones prácticas en varios campos del conocimiento.
Preguntas Frecuentes
¿Cuáles son algunos ejemplos ilustrativos de imágenes de funciones matemáticas en diferentes contextos?
Algunos ejemplos ilustrativos de imágenes de funciones matemáticas en diferentes contextos incluyen:
1. Gráfica de una parábola: Representa la función cuadrática f(x) = ax² + bx + c, utilizada en la física para describir el movimiento de proyectiles.
2. Curva sinusoidal: Muestra la función f(x) = sin(x), comúnmente aplicada en la música y señales de audio.
3. Exponencial creciente: La función f(x) = e^x se utiliza en finanzas para modelar el crecimiento del interés compuesto.
4. Función logarítmica: Gráfica de f(x) = log(x), utilizada en escalas como el pH o la escala Richter de terremotos.
Estos ejemplos muestran cómo las funciones matemáticas se aplican en diversas disciplinas, facilitando la comprensión de fenómenos reales.
¿Cómo se determina la imagen de una función a partir de su representación gráfica?
La imagen de una función se determina al observar su representación gráfica. En el gráfico, la imagen corresponde a todos los valores de salida (ejes y) que se obtienen para cada valor de entrada (ejes x). Para identificarla, se pueden trazar líneas horizontales y ver qué puntos de intersección existen con la curva. Todos estos puntos en el eje y forman el conjunto de la imagen de la función.
¿Qué ejemplos existen que muestren la relación entre la imagen de una función y su dominio?
Existen varios ejemplos que muestran la relación entre la imagen de una función y su dominio. Por ejemplo, en la función cuadrática ( f(x) = x^2 ), el dominio son todos los números reales ( (-infty, +infty) ), mientras que la imagen es ( [0, +infty) ) porque solo toma valores no negativos. Otro ejemplo es la función ( f(x) = sqrt{x} ), cuyo dominio es ( [0, +infty) ) y su imagen también es ( [0, +infty) ). Estos ejemplos ilustran cómo el dominio y la imagen están interrelacionados.
¿En qué situaciones se pueden aplicar ejemplos de imágenes de funciones en la resolución de problemas matemáticos?
Los ejemplos de imágenes de funciones se pueden aplicar en situaciones como:
1. Gráficas de funciones: Para visualizar el comportamiento de una función y entender su tendencia.
2. Problemas de optimización: Al mostrar máximos y mínimos de una función a través de su representación gráfica.
3. Interpretación de datos: Para ilustrar relaciones entre variables en análisis estadísticos.
4. Resolución de ecuaciones: Al graficar funciones para encontrar puntos de intersección que representan soluciones.
Estos ejemplos ayudan a comprender mejor y resolver problemas matemáticos de manera más efectiva.
En conclusión, comprender la imagen de una función es fundamental para el estudio de las matemáticas. Los ejemplos presentados ilustran su aplicación en diversas áreas. Te invitamos a compartir este contenido y a seguir explorando más artículos que profundizan en este fascinante tema. ¡Sigue aprendiendo con nosotros!