La función homográfica es una herramienta matemática de gran relevancia en el análisis de relaciones entre variables. Este artículo se adentra en sus ejemplos prácticos, desglosando cómo esta función se manifiesta en diversas áreas del conocimiento, desde la economía hasta la ingeniería.
A través de un enfoque riguroso y detallado, exploraremos las características fundamentales de la función homográfica y su aplicación en problemas reales.
¡Sigue leyendo para descubrir cómo dominar este concepto esencial!
Contenido
### Ejemplos Clave de Funciones Homográficas: Aplicaciones y Gráficas Explicativas
Las funciones homográficas son una clase de funciones racionales que se expresan en la forma general:
f(x) = (ax + b) / (cx + d)
donde a, b, c y d son constantes, y con la condición de que c y d no sean simultáneamente cero. Estas funciones presentan características particulares que las hacen útiles en diversos campos, desde la economía hasta la física. A continuación, se presentan ejemplos clave de sus aplicaciones y gráficas explicativas.
- Economía: En economía, las funciones homográficas se utilizan para modelar la relación entre oferta y demanda. Por ejemplo, la función de precio puede expresarse como:
- f(p) = (a * p + b) / (c * p + d)
- Óptica: En óptica, estas funciones son útiles para describir la relación entre la distancia del objeto y la distancia de la imagen producida por una lente. La fórmula:
- f(d) = (m * d) / (n * d + p)
- Ingeniería: En ingeniería, las funciones homográficas pueden ser aplicadas en el análisis de sistemas de control. Por ejemplo, el comportamiento de un sistema se puede modelar como:
- f(t) = (kt + m) / (nt + p)
donde p representa el precio de un bien. Esta relación permite determinar el equilibrio del mercado.
ayuda a calcular el aumento de la imagen en función de la distancia del objeto.
donde t es el tiempo, permitiendo optimizar el rendimiento de sistemas dinámicos.
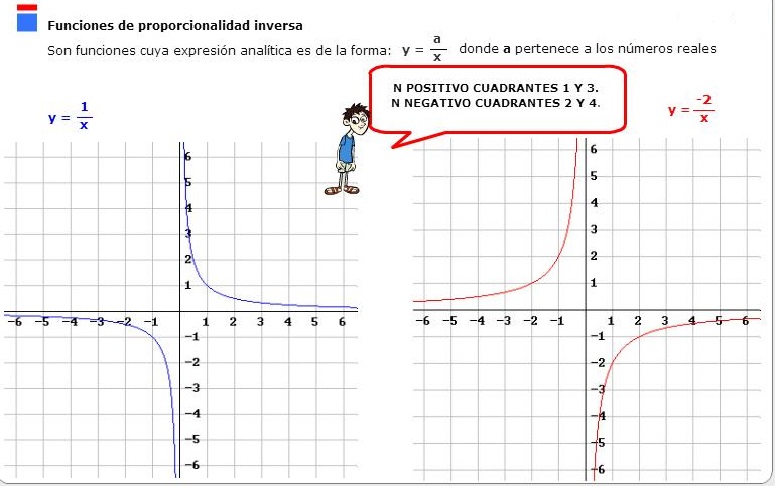
La gráfica de una función homográfica tiene características distintivas:
- Asintotas: Las funciones homográficas presentan asintotas verticales y horizontales. La asintota vertical ocurre cuando el denominador se anula (cx + d = 0), mientras que la asintota horizontal se establece conforme x tiende a infinito, siendo f(x) = a/c.
- Puntos de intersección: La función puede intersectar los ejes coordenados. Para hallar la intersección con el eje y, se evalúa f(0) = b/d, y para el eje x, se resuelve ax + b = 0.
- Dominio y rango: El dominio de la función excluye los valores que hacen el denominador igual a cero. Por otro lado, el rango dependerá de las asintotas y los puntos críticos de la función.
Las funciones homográficas no solo son fundamentales en matemáticas puras, sino que también tienen aplicaciones prácticas en la vida cotidiana. Su versatilidad y capacidad para modelar relaciones complejas las convierten en herramientas esenciales para el análisis en diversas disciplinas.
Definición de la Función Homográfica
La función homográfica, también conocida como función racional, se define como una relación matemática en la que una variable dependiente ( y ) se expresa en términos de una variable independiente ( x ) mediante una fracción. Esta fracción tiene un numerador y un denominador que son ambos polinomios de primer grado. La forma general de una función homográfica es:
[
y = frac{ax + b}{cx + d}
]
donde ( a ), ( b ), ( c ) y ( d ) son constantes, y ( cx + d neq 0 ). Esta función es fundamental en el análisis matemático debido a sus propiedades particulares, como la existencia de asíntotas y su comportamiento en diferentes intervalos.
Características Principales
Las funciones homográficas presentan varias características importantes que las distinguen de otras funciones algebraicas. Entre ellas se encuentran:
- Asíntotas: Estas funciones pueden tener asíntotas verticales y horizontales, que son líneas que la gráfica de la función se aproxima pero nunca toca.
- Dominio y rango: El dominio de una función homográfica excluye los valores que hacen que el denominador sea cero, mientras que el rango puede abarcar todos los números reales excepto el valor de la asíntota horizontal.
- Intersecciones: Las intersecciones con los ejes se determinan al igualar la función a cero o al evaluar la función en cero.
Estas características permiten estudiar el comportamiento y la naturaleza de las funciones homográficas en diferentes contextos.
Ejemplos de Funciones Homográficas
Para ilustrar la aplicación de la función homográfica, a continuación se presentan algunos ejemplos representativos:
-
Ejemplo 1: ( y = frac{2x + 3}{x – 1} )
- El numerador ( 2x + 3 ) y el denominador ( x – 1 ) son ambos polinomios de primer grado.
- La asíntota vertical ocurre en ( x = 1 ) y la asíntota horizontal es ( y = 2 ).
-
Ejemplo 2: ( y = frac{5x – 2}{3x + 4} )
- En este caso, la asíntota vertical se encuentra en ( x = -frac{4}{3} ) y la asíntota horizontal es ( y = frac{5}{3} ).
- Este tipo de funciones se utilizan frecuentemente en modelos económicos y físicos.
Estos ejemplos son esenciales para comprender cómo se comportan las funciones homográficas en diferentes situaciones y cómo se aplican en diversas áreas del conocimiento.
Aplicaciones de la Función Homográfica
Las funciones homográficas tienen aplicaciones en diversas disciplinas, incluyendo la economía, la física y la ingeniería. Su importancia radica en la capacidad de modelar situaciones reales que involucran relaciones inversas o proporcionalidades.
En Economía
En el contexto económico, las funciones homográficas se utilizan para representar la relación entre la oferta y la demanda. Por ejemplo, se pueden emplear para modelar el precio de un artículo en función de la cantidad ofrecida. Esto permite a los economistas predecir cómo cambios en la oferta afectarán los precios de mercado y, por ende, la economía en general.
En Física
En el ámbito físico, estas funciones pueden describir fenómenos como la velocidad de un objeto en movimiento en función del tiempo. Por ejemplo, al analizar el movimiento de un proyectil, se puede utilizar una función homográfica para modelar la trayectoria tomando en cuenta la resistencia del aire y otros factores.
En Ingeniería
Los ingenieros también recurren a funciones homográficas para diseñar sistemas de control y optimización de procesos. Por ejemplo, en la calibración de instrumentos de medida, es común usar funciones homográficas para ajustar las lecturas y mejorar la precisión de los dispositivos.
Gráfica de una Función Homográfica
La representación gráfica de una función homográfica es esencial para estudiar su comportamiento y características. La gráfica es una curva que puede exhibir diferentes formas dependiendo de los coeficientes del numerador y el denominador.
Elementos de la Gráfica
Al graficar una función homográfica, se deben considerar varios elementos clave:
- Puntos de intersección: La gráfica intersecta el eje ( y ) en ( b/d ) y el eje ( x ) en ( -b/a ).
- Asíntotas: Se debe trazar la línea de la asíntota vertical donde el denominador se anula y la asíntota horizontal que se determina a partir de los coeficientes de los polinomios.
- Comportamiento en intervalos: Es importante examinar el comportamiento de la función en diferentes intervalos alrededor de las asíntotas.
La comprensión de estos elementos es crucial para el análisis de la función y su aplicación en diversos contextos científicos y académicos.
Conclusiones sobre la Función Homográfica
En resumen, la función homográfica es una herramienta matemática poderosa que permite modelar una amplia variedad de situaciones en diferentes campos del conocimiento. Desde su definición y características hasta sus aplicaciones prácticas, la función homográfica proporciona un marco para entender relaciones complejas.
Su estudio no solo es relevante para las matemáticas puras, sino que también tiene implicaciones significativas en áreas aplicadas como la economía, la física y la ingeniería. Por lo tanto, es fundamental continuar explorando sus propiedades y aplicaciones para aprovechar al máximo su potencial en la resolución de problemas reales.
Preguntas Frecuentes
¿Cuáles son algunos ejemplos prácticos de funciones homográficas en la resolución de problemas matemáticos?
Algunos ejemplos prácticos de funciones homográficas en la resolución de problemas matemáticos incluyen:
1. Problemas de proporcionalidad: Se utilizan para calcular tasas de cambio, como la velocidad en relación a la distancia y el tiempo.
2. Modelado de situaciones reales: Por ejemplo, la relación entre la altura de un objeto y su sombra en un día soleado puede representarse con una función homográfica.
3. Economía: En el análisis de costos y beneficios, se pueden emplear para determinar el precio óptimo de un producto en función de la demanda.
Estas funciones son útiles para simplificar cálculos y visualizar relaciones complejas entre variables.
¿Cómo se pueden aplicar las funciones homográficas en contextos del mundo real, como la economía o la física?
Las funciones homográficas se pueden aplicar en diversos contextos del mundo real. En economía, por ejemplo, se utilizan para modelar la relación entre el precio y la demanda de un producto; a medida que el precio cambia, la demanda puede variar de manera no lineal, lo que se puede representar con una función homográfica. En física, estas funciones son útiles para describir fenómenos como la trayectoria de un proyectil, donde la relación entre la altura y la distancia recorrida puede ser expresada mediante una función de este tipo. Así, las funciones homográficas permiten entender y predecir comportamientos complejos en diferentes disciplinas.
¿Qué características distintivas presentan los gráficos de funciones homográficas en comparación con otras funciones racionales?
Los gráficos de funciones homográficas, que son del tipo ( f(x) = frac{ax + b}{cx + d} ), presentan características distintivas como:
1. Asintotas: Tienen asintotas verticales y asintotas horizontales que dependen de los coeficientes ( c ) y ( a ).
2. Forma de la curva: Suelen mostrar un comportamiento similar a una hipérbola, dividiéndose en dos ramas.
3. Intersecciones: Pueden tener intersecciones con los ejes que son diferentes a otras funciones racionales.
Estas características les confieren un comportamiento único en comparación con otras funciones racionales.
¿Cómo se derivan y analizan los ejemplos de funciones homográficas en el estudio de las transformaciones geométricas?
Las funciones homográficas, que se expresan como f(x) = (ax + b) / (cx + d), se derivan al considerar la relación entre las coordenadas de puntos en el plano. En el estudio de transformaciones geométricas, estas funciones permiten realizar transformaciones como traslaciones, escalados y rotaciones. Al analizar sus propiedades, como la continuidad y la existencia de asíntotas, se pueden comprender mejor cómo afectan a las figuras geométricas, facilitando su representación y manipulación en contextos matemáticos y gráficos.
En conclusión, la función homográfica es fundamental en diversas aplicaciones matemáticas y científicas. Los ejemplos analizados ilustran su relevancia y versatilidad. Te invitamos a compartir este contenido y a seguir explorando más sobre este tema fascinante en nuestros próximos artículos. ¡Tu curiosidad es el primer paso hacia el conocimiento!