Ejemplos De Vectores En La Vida Cotidiana Que No Te Puedes Perder

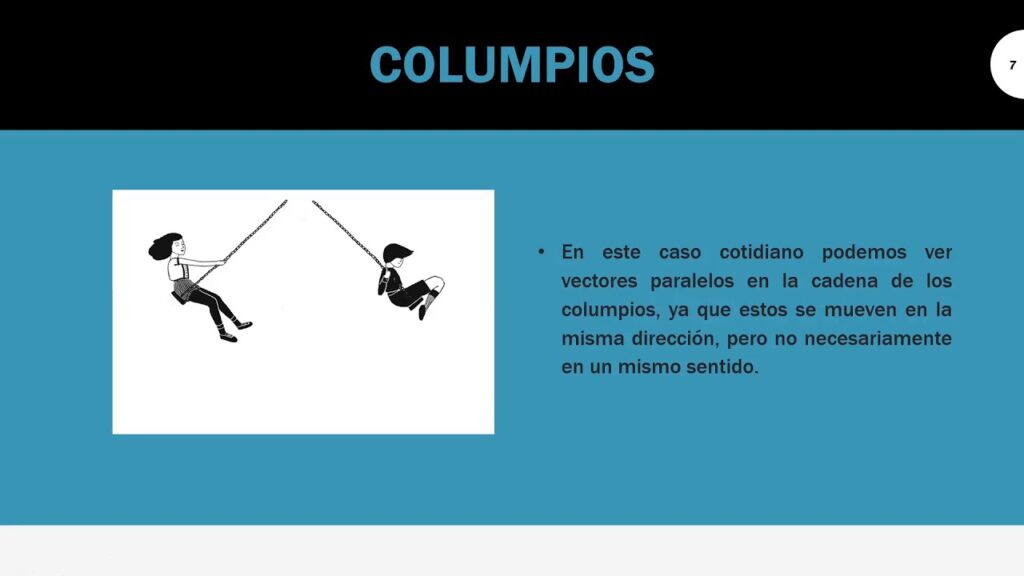
En el fascinante mundo de la física y las matemáticas, los vectores juegan un papel crucial que se refleja en nuestra vida cotidiana. Desde la dirección del viento hasta el desplazamiento de un automóvil, estos elementos son fundamentales para comprender fenómenos cotidianos.
Este artículo explorará diversos ejemplos de vectores en situaciones diarias, revelando cómo estos conceptos abstractos se materializan en experiencias tangibles y esenciales.
Acompáñanos en este recorrido y descubre la interconexión entre matemáticas y la realidad que nos rodea.

Descubriendo los Vectores: Ejemplos Cotidianos que Ilustran su Aplicación en Nuestra Vida Diaria

Los vectores son entidades matemáticas que poseen tanto magnitud como dirección, y su aplicación se encuentra en múltiples aspectos de nuestra vida diaria. A continuación, se presentan ejemplos cotidianos que ilustran cómo interactuamos con los vectores sin ser conscientes de ello.

• Transporte y Navegación: Cuando utilizamos un GPS, este sistema calcula la ruta más eficiente entre dos puntos. Aquí, las posiciones geográficas pueden representarse como vectores, donde cada vector indica la dirección y la distancia a seguir. Por ejemplo, un viaje en coche desde una ciudad a otra puede descomponerse en vectores que representen cada tramo del recorrido.
• Deportes: En el ámbito deportivo, los vectores son fundamentales para analizar el rendimiento de los atletas. En el baloncesto, por ejemplo, el lanzamiento de la pelota se puede describir mediante un vector que indique la fuerza y la dirección del tiro. La velocidad y la dirección del balón son componentes vectoriales que determinan si el tiro será exitoso.
• Física y Movimiento: Los conceptos de velocidad y aceleración son inherentemente vectoriales. Al conducir un vehículo, la velocidad no solo se mide por cuántos kilómetros se recorren, sino también por la dirección en la que se mueve el automóvil. Un cambio en la dirección del movimiento implica un cambio en el vector de velocidad.
• Ingeniería y Diseño: En ingeniería, los vectores son utilizados para modelar fuerzas que actúan sobre estructuras. Por ejemplo, al diseñar un puente, los ingenieros deben considerar los vectores que representan el peso de la estructura y las fuerzas del viento, asegurando que estas fuerzas se equilibren adecuadamente para garantizar la estabilidad.

Además de estos ejemplos, los vectores también se encuentran en:

• Gráficos por Computadora: En la creación de gráficos y animaciones, los objetos se mueven a través de un espacio tridimensional utilizando vectores para definir su posición y dirección.
• Sonido y Música: Las ondas sonoras pueden ser representadas mediante vectores en un espacio de frecuencia, donde cada frecuencia tiene una magnitud y dirección específica, afectando así la percepción del sonido.
• Climatología: Los meteorólogos utilizan vectores para representar la dirección y velocidad del viento, lo que es vital para prever condiciones climáticas y emitir alertas tempranas.

Estos ejemplos evidencian cómo los vectores son fundamentales en diversas disciplinas y situaciones cotidianas, proporcionando un marco para entender y describir fenómenos que involucren tanto magnitud como dirección. La capacidad de aplicar conceptos vectoriales en situaciones reales no solo facilita la resolución de problemas, sino que también amplía nuestra comprensión del mundo que nos rodea.

Definición de vectores en física y matemáticas

Concepto básico de vectores

Un vector es una entidad matemática que tiene tanto magnitud como dirección. En el contexto de la física, los vectores son fundamentales para describir fenómenos como el movimiento, la fuerza y el campo eléctrico. A diferencia de un escalar, que solo tiene magnitud (como la temperatura), un vector proporciona información más completa sobre cómo se comportan las cantidades en el espacio.

Representación gráfica de vectores

Los vectores se representan comúnmente mediante flechas en un plano cartesiano. La longitud de la flecha indica su magnitud, mientras que la dirección de la flecha señala hacia dónde apunta el vector. Esto permite visualizar fácilmente cómo interactúan diferentes fuerzas o velocidades en un sistema. Para representar un vector, se utilizan coordenadas cartesianas, donde los ejes X e Y especifican su posición y dirección.

Ejemplos de vectores en matemáticas

En matemáticas, los vectores se utilizan en diversas áreas, desde álgebra lineal hasta cálculo. Algunos ejemplos incluyen:

• Vectores en el espacio tridimensional: Representan posiciones o movimientos en tres dimensiones.
• Vectores unitarios: Son vectores con una magnitud de uno, utilizados para indicar dirección.
• Operaciones con vectores: Como la suma y la multiplicación de vectores, que tienen aplicaciones en diversas disciplinas.

Ejemplos de vectores en el deporte

Dirección y velocidad en el fútbol

En el fútbol, el concepto de vector se aplica a la dirección y la velocidad del balón. Cuando un jugador patea el balón, no solo se considera la fuerza aplicada (magnitud), sino también la dirección en la que se envía el balón. Esto es crucial para calcular trayectorias y realizar estrategias efectivas durante el juego.

Aceleración y movimiento en el atletismo

En el atletismo, los corredores experimentan cambios en su aceleración y velocidad que se pueden representar mediante vectores. La dirección en la que corren y la rapidez con que aumentan o disminuyen su velocidad son ejemplos claros de cómo los vectores influyen en el rendimiento deportivo. Los entrenadores pueden utilizar estos datos para optimizar el rendimiento de los atletas.

Fuerzas en competiciones de equipo

En deportes de equipo como el baloncesto o el rugby, cada jugador ejerce fuerzas que afectan el movimiento del balón. Estas fuerzas pueden ser representadas como vectores que permiten analizar el juego desde una perspectiva física. Por ejemplo, el análisis de la dirección y la magnitud de las fuerzas aplicadas puede ayudar a entender mejor las dinámicas del juego y mejorar las tácticas.

Aplicaciones de vectores en la navegación

Navegación marítima

En la navegación marítima, los vectores son esenciales para determinar la posición y el rumbo de un barco. Los capitanes utilizan vectores para calcular la dirección y la velocidad del viento, así como las corrientes marinas. Esto permite trazar rutas eficientes y seguras, minimizando riesgos durante la travesía.

Navegación aérea

De manera similar, los aviones emplean vectores en sus sistemas de navegación. Los pilotos deben considerar varios vectores, incluyendo la velocidad del aire, la dirección del vuelo y las corrientes de aire. Estos factores son cruciales para ajustar el rumbo y asegurar un vuelo seguro y eficiente.

Uso de tecnología GPS

La tecnología GPS (Sistema de Posicionamiento Global) también se basa en principios de vectores. Los satélites transmiten señales que permiten calcular la posicionamiento exacto de un objeto en la superficie terrestre. Este sistema utiliza vectores para determinar la distancia y la dirección hacia el destino, facilitando la navegación en diversas aplicaciones, desde vehículos hasta dispositivos móviles.

Vectores en la ingeniería y la arquitectura

Diseño estructural

En ingeniería y arquitectura, los vectores desempeñan un papel crucial en el diseño estructural. Los ingenieros utilizan vectores para analizar las cargas y fuerzas que actúan sobre un edificio o puente. Esto permite garantizar la estabilidad y seguridad de las estructuras, diseñando elementos que puedan soportar las tensiones aplicadas.

Simulación y modelado 3D

El uso de software de modelado 3D en arquitectura requiere el manejo de vectores para representar objetos en el espacio tridimensional. Cada elemento del diseño arquitectónico se puede describir mediante vectores que definen su forma, tamaño y posición. Esto permite a los arquitectos visualizar y manipular sus diseños de manera efectiva.

Control de maquinaria

En la ingeniería mecánica, los vectores son fundamentales para controlar la movilidad de máquinas y robots. Los sistemas de control utilizan algoritmos que consideran vectores de posición y velocidad para garantizar un funcionamiento preciso. Esto es particularmente importante en la automatización industrial, donde se requiere alta precisión y eficiencia.

Conclusiones sobre el uso de vectores en la vida cotidiana

Integración de vectores en diversas disciplinas

Los vectores son una herramienta fundamental en numerosas disciplinas, desde la física y las matemáticas hasta la ingeniería y la navegación. Su capacidad para representar tanto magnitud como dirección permite a los profesionales analizar y resolver problemas complejos de manera efectiva. La comprensión de los vectores es esencial para quienes buscan aplicar conceptos científicos en situaciones prácticas.

Importancia en la educación y la investigación

El estudio de los vectores es crucial en la educación, ya que proporciona una base sólida para entender conceptos más avanzados en ciencias y matemáticas. Además, la investigación en campos como la física aplicada y la ingeniería continúa explorando nuevas formas de utilizar vectores para desarrollar tecnologías innovadoras y soluciones sostenibles.

Perspectivas futuras sobre el uso de vectores

A medida que la tecnología avanza, es probable que surjan nuevas aplicaciones para los vectores. Desde la inteligencia artificial hasta la robótica, la necesidad de comprender y utilizar vectores será cada vez más relevante. Por lo tanto, tanto educadores como investigadores deben seguir promoviendo el estudio de los vectores como un aspecto clave en el desarrollo científico y tecnológico del futuro.

Preguntas Frecuentes

¿Cuáles son algunos ejemplos de vectores que se pueden observar en la naturaleza y cómo se manifiestan en fenómenos físicos?

Algunos ejemplos de vectores en la naturaleza incluyen:

1. Fuerza Gravitacional: La atracción entre dos cuerpos, como la Tierra y un objeto que cae.
2. Viento: Representa tanto dirección como velocidad, influyendo en fenómenos meteorológicos.
3. Corrientes Oceánicas: Mueven grandes masas de agua, afectando el clima y la vida marina.
4. Desplazamiento de Animales: Los migratorios utilizan vectores para orientarse en sus rutas.

Estos ejemplos muestran cómo los vectores son esenciales para entender el movimiento y las interacciones en el entorno natural.

¿De qué manera los vectores son utilizados en la ingeniería para resolver problemas prácticos en el diseño de estructuras?

Los vectores son esenciales en la ingeniería para resolver problemas prácticos en el diseño de estructuras. Por ejemplo, se utilizan para representar fuerzas que actúan sobre un edificio, permitiendo a los ingenieros calcular el equilibrio y la estabilidad de la estructura. Además, los vectores ayudan a determinar direcciones y magnitudes en análisis estructurales, como en el caso de puentes o vigas, garantizando que puedan soportar cargas dinámicas y estáticas sin fallar.

¿Cómo se aplican los conceptos de vectores en la navegación marítima y aérea?

En la navegación marítima y aérea, los conceptos de vectores se aplican para determinar rutas y direcciones. Por ejemplo, un barco utiliza vectores para calcular su velocidad y dirección en relación con las corrientes marinas y el viento. De igual manera, un avión emplea vectores de viento y curso para ajustar su trayectoria y mantener el rumbo deseado. Estos cálculos permiten optimizar el combustible y mejorar la seguridad del viaje.

¿Qué ejemplos de vectores se pueden encontrar en el ámbito deportivo y cómo influyen en el rendimiento de los atletas?

En el ámbito deportivo, algunos ejemplos de vectores son:

1. Fuerza: La dirección y magnitud de la fuerza aplicada al saltar o lanzar influyen directamente en el rendimiento.
2. Velocidad: La velocidad de un corredor se representa como un vector, afectando su capacidad para completar una carrera.
3. Aceleración: El cambio en la velocidad de un atleta durante una competición es fundamental para optimizar su rendimiento.

Estos vectores son cruciales ya que determinan la eficacia en la ejecución de movimientos y pueden ser analizados para mejorar técnicas y entrenamientos.

En conclusión, los vectores son fundamentales en diversas actividades cotidianas, desde el deporte hasta la tecnología. Reconocer su presencia nos ayuda a entender mejor el mundo que nos rodea. Te invitamos a compartir este artículo y a seguir explorando más sobre fenómenos científicos en nuestra plataforma. ¡Tu curiosidad es clave para el aprendizaje!