En el estudio de la matemática vectorial, la suma de vectores en el plano cartesiano es un concepto fundamental que permite entender cómo se combinan diferentes magnitudes y direcciones. A través de este artículo, exploraremos diversos ejemplos prácticos que ilustran este proceso, facilitando la comprensión de la representación gráfica y algebraica de los vectores.
A medida que avancemos, desglosaremos cada ejemplo, proporcionando una base sólida para aquellos que deseen profundizar en esta temática esencial. ¡Sigue leyendo para descubrir cómo los vectores pueden transformarse y sumarse en el fascinante mundo del plano cartesiano!
Contenido
- Ejemplos Prácticos de Suma de Vectores en el Plano Cartesiano: Aplicaciones y Ejercicios Resueltos
- Definición de Vectores en el Plano Cartesiano
- Suma de Vectores: Principios Fundamentales
- Ejemplos Prácticos de Suma de Vectores
- Aplicaciones de la Suma de Vectores
- Conclusiones sobre la Suma de Vectores
- Preguntas Frecuentes
Ejemplos Prácticos de Suma de Vectores en el Plano Cartesiano: Aplicaciones y Ejercicios Resueltos
La suma de vectores es una operación fundamental en el estudio de la física y la ingeniería, especialmente cuando se trabaja en el plano cartesiano. A continuación, se presentan ejemplos prácticos que ilustran cómo se realiza esta operación y sus aplicaciones.
Ejemplo 1: Suma de dos vectores
Supongamos que tenemos dos vectores en el plano cartesiano:
- Vector A = (3, 4)
- Vector B = (1, 2)
Para sumar estos vectores, se deben sumar las componentes correspondientes:
[
text{Vector Resultante} = text{Vector A} + text{Vector B} = (3+1, 4+2) = (4, 6)
]
La suma de los vectores A y B da como resultado un nuevo vector, que podemos denotar como C = (4, 6).
Ejemplo 2: Aplicación en la física
Consideremos un caso práctico en física donde dos fuerzas actúan sobre un objeto. Sea:
- Fuerza F1 = (5 N, 0 N) [hacia la derecha]
- Fuerza F2 = (0 N, 3 N) [hacia arriba]
La suma de estas fuerzas se realiza de la misma manera:
[
text{Fuerza Resultante} = text{Fuerza F1} + text{Fuerza F2} = (5+0, 0+3) = (5 N, 3 N)
]
Esto nos indica que el objeto experimentará una fuerza resultante de 5 N hacia la derecha y 3 N hacia arriba.
Ejemplo 3: Uso de la representación gráfica
La representación gráfica de la suma de vectores también es esencial. Para ilustrarlo, consideremos los siguientes pasos:
- Dibuja el vector A en un sistema de coordenadas.
- Desde la punta del vector A, dibuja el vector B.
- La línea desde el origen hasta la punta del vector B representa la suma de los vectores.
Este método gráfico es útil para visualizar la dirección y magnitud de la suma de vectores.
Ejercicio Resuelto
Calculemos la suma de los siguientes vectores:
- Vector D = (2, -3)
- Vector E = (-1, 4)
La suma se lleva a cabo de la siguiente manera:
[
text{Vector Resultante} = text{Vector D} + text{Vector E} = (2-1, -3+4) = (1, 1)
]
La suma de los vectores D y E resulta en un nuevo vector F = (1, 1).
Aplicaciones en ingeniería y navegación
En ingeniería y navegación, la suma de vectores es crucial para determinar trayectorias y fuerzas resultantes. Algunos ejemplos incluyen:
- Cálculo de la trayectoria de un proyectil.
- Determinación de la fuerza neta en estructuras.
- Orientación de vehículos en navegación aérea y marítima.
Estos ejemplos ilustran la importancia de la suma de vectores en diversos campos, mostrando su relevancia tanto teórica como práctica.
Definición de Vectores en el Plano Cartesiano
Concepto de Vector
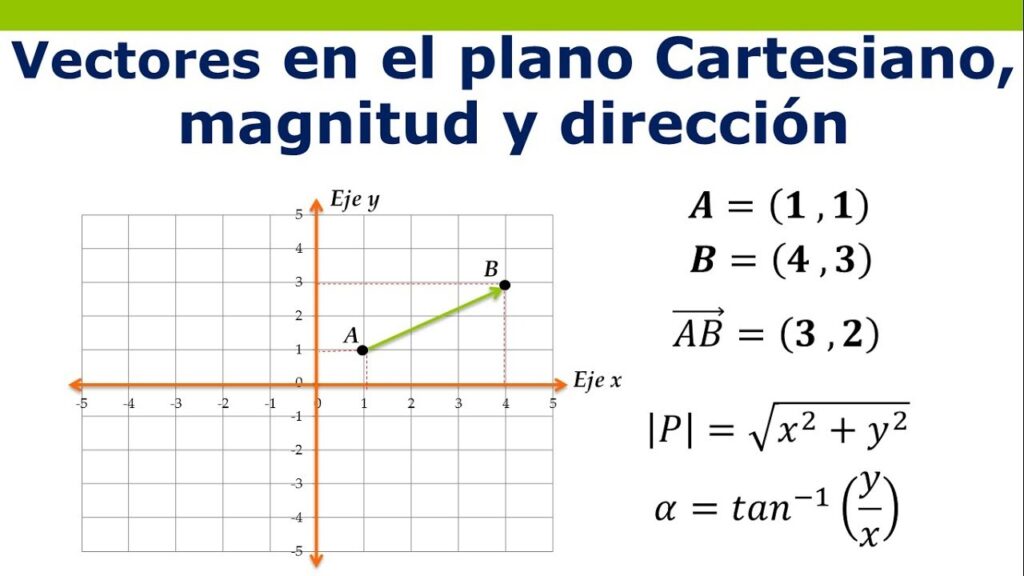
Un vector es una entidad matemática que tiene tanto magnitud como dirección. En el plano cartesiano, un vector se puede representar como un par de coordenadas (x, y), donde x es la componente horizontal y y es la componente vertical. Por ejemplo, un vector A con coordenadas (3, 4) indica que se desplaza 3 unidades en la dirección x y 4 unidades en la dirección y.
Representación Gráfica de Vectores
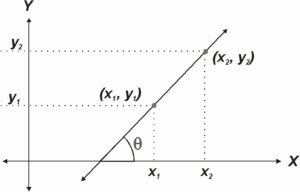
La representación gráfica de un vector en el plano cartesiano se realiza mediante una flecha dirigida desde el origen (0, 0) hasta el punto definido por sus coordenadas. Esta flecha no solo muestra la dirección del vector, sino también su longitud, que corresponde a su magnitud. La longitud se puede calcular utilizando el teorema de Pitágoras, dado que:
- Magnitud = √(x² + y²)
Esta representación visual es fundamental para entender la suma de vectores, ya que permite ver cómo se combinan sus direcciones y magnitudes.
Suma de Vectores: Principios Fundamentales
Propiedades de la Suma de Vectores
La suma de vectores sigue ciertas propiedades que son cruciales para su comprensión. Las más relevantes son:
- Conmutatividad: A + B = B + A
- Asociatividad: (A + B) + C = A + (B + C)
- Elemento Neutro: A + 0 = A
Estas propiedades garantizan que la suma de vectores sea consistente y predecible, facilitando el análisis de problemas complejos en diversas áreas de la física y la ingeniería.
Métodos de Suma de Vectores
Existen dos métodos principales para sumar vectores en el plano cartesiano: el método gráfico y el método analítico.
- Método Gráfico: Se utiliza el diagrama de flechas donde se coloca un vector al final del otro, formando un triángulo o un paralelogramo.
- Método Analítico: Se suman las componentes correspondientes de los vectores. Si A = (x₁, y₁) y B = (x₂, y₂), entonces A + B = (x₁ + x₂, y₁ + y₂).
Ambos métodos son igualmente válidos, pero el análisis analítico es preferido en situaciones que requieren mayor precisión.
Ejemplos Prácticos de Suma de Vectores
Ejemplo 1: Suma Gráfica de Vectores
Supongamos que tenemos dos vectores: A = (2, 3) y B = (4, 1). Para sumar estos vectores gráficamente, dibujamos el vector A desde el origen hasta el punto (2, 3) y luego el vector B desde el extremo del vector A hasta el punto (6, 4). El vector resultante R va del origen hasta el punto (6, 4).
Ejemplo 2: Suma Analítica de Vectores
Utilizando el mismo ejemplo anterior, podemos realizar la suma analítica. Para ello, sumamos las componentes de ambos vectores:
- Componente x: 2 + 4 = 6
- Componente y: 3 + 1 = 4
Por lo tanto, el vector resultante R es R = (6, 4), confirmando la suma realizada gráficamente.
Aplicaciones de la Suma de Vectores
Uso en Física
La suma de vectores es esencial en el campo de la física, especialmente en el análisis de fuerzas. Por ejemplo, si dos fuerzas actúan sobre un objeto en direcciones diferentes, la suma de estas fuerzas determinará la aceleración del objeto según la segunda ley de Newton (F = ma). Este concepto es aplicable en situaciones cotidianas como el movimiento de vehículos, deportes y estructuras ingenieriles.
Uso en Ingeniería
En ingeniería, la suma de vectores es utilizada para resolver problemas de estática y dinámica. Por ejemplo, al diseñar un puente, los ingenieros deben calcular las fuerzas que actúan en diferentes puntos del puente, asegurando que la estructura sea capaz de soportar estas fuerzas combinadas. Esto implica sumar múltiples vectores que representan diferentes cargas y fuerzas.
Conclusiones sobre la Suma de Vectores
Importancia de Comprender la Suma de Vectores
Entender cómo sumar vectores en el plano cartesiano es fundamental para cualquier estudiante de matemáticas, física o ingeniería. No solo proporciona herramientas para resolver problemas complejos, sino que también ofrece una base sólida para conceptos más avanzados en estas disciplinas.
Perspectivas Futuras
Con el avance de la tecnología, la aplicación de la suma de vectores se ha expandido a campos como la informática y la robótica. Sistemas de navegación y algoritmos de inteligencia artificial utilizan principios de suma de vectores para procesar información espacial y tomar decisiones. Por lo tanto, el estudio de la suma de vectores seguirá siendo relevante en el futuro.
Preguntas Frecuentes
¿Cuáles son los pasos para realizar la suma de vectores en el plano cartesiano utilizando el método gráfico?
Para realizar la suma de vectores en el plano cartesiano utilizando el método gráfico, sigue estos pasos:
1. Dibuja el primer vector: Comienza en un punto de origen y dibuja el vector en la dirección y con la magnitud correspondientes.
2. Dibuja el segundo vector: Coloca el inicio del segundo vector en la punta del primero, manteniendo su dirección y magnitud.
3. Traza la diagonal: Desde el punto de origen del primer vector hasta la punta del segundo vector, dibuja una línea recta. Esta línea representa la suma de los vectores.
4. Analiza el resultado: La longitud y dirección de esta línea indican la magnitud y dirección del vector resultante.
Recuerda que este método es visual y te ayuda a comprender mejor la interacción entre vectores.
¿Cómo se aplica el teorema de Pitágoras en la suma de vectores en el plano cartesiano?
El teorema de Pitágoras se aplica en la suma de vectores en el plano cartesiano para encontrar la magnitud del vector resultante. Si tienes dos vectores, A y B, que forman un ángulo recto, puedes calcular su suma utilizando la fórmula:
R = √(A² + B²),
donde R es la magnitud del vector resultante. Por ejemplo, si A tiene una longitud de 3 unidades y B tiene 4 unidades, la magnitud del vector resultante será:
R = √(3² + 4²) = √(9 + 16) = √25 = 5.
¿Qué ejemplos ilustran la suma de vectores en situaciones físicas, como la fuerza y el desplazamiento?
Un ejemplo de la suma de vectores en situaciones físicas es el desplazamiento de un barco. Si un barco navega 10 km al norte y luego 5 km al este, el desplazamiento total se obtiene sumando estos vectores, resultando en un desplazamiento diagonal.
Otro ejemplo es la fuerza neta sobre un objeto. Si se aplican dos fuerzas de 10 N hacia la derecha y 5 N hacia la izquierda, la fuerza neta se calcula sumando estos vectores, dando como resultado 5 N hacia la derecha.
¿De qué manera se pueden representar las componentes de vectores en una suma en el plano cartesiano?
Las componentes de vectores en una suma en el plano cartesiano se pueden representar mediante el uso de ejes coordenados. Cada vector se descompone en sus componentes x y y, que se grafican desde el origen. La suma de los vectores se obtiene al sumar las componentes correspondientes: (R_x = A_x + B_x) y (R_y = A_y + B_y). Finalmente, el vector resultante se dibuja desde el origen hasta el punto (R_x, R_y).
En conclusión, la suma de vectores en el plano cartesiano es fundamental para comprender diversas aplicaciones en física y matemáticas. A través de ejemplos concretos, hemos ilustrado su importancia. Te invitamos a compartir este contenido y a seguir explorando más sobre este fascinante tema en nuestros próximos artículos.