¿Necesitas entender y resolver ecuaciones completas? En este artículo te presentamos una selección de ejemplos que te ayudarán a dominar este tema. A través de explicaciones claras y concisas, podrás comprender el proceso paso a paso y aplicarlo a cualquier problema que se te presente. ¡Descubre cómo las ecuaciones completas pueden simplificar tus cálculos matemáticos!
Contenido
Ejemplos de Ecuaciones Completas
Las ecuaciones completas son expresiones matemáticas que contienen tanto coeficientes como variables y constantes. En otras palabras, son ecuaciones en las que todas las incógnitas están presentes.
A continuación, se presentan algunos ejemplos de ecuaciones completas:
1. Ecuación lineal: Una ecuación lineal es aquella en la que la variable está elevada a la primera potencia y no hay términos con exponentes mayores. Por ejemplo:
- 2x + 5 = 10
- 3y – 2 = y + 4
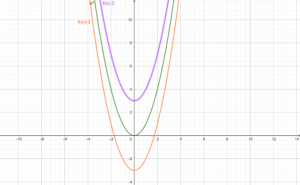
2. Ecuación cuadrática: Una ecuación cuadrática es aquella en la que la variable está elevada al cuadrado. Por ejemplo:
- x^2 + 3x + 2 = 0
- 2y^2 – 5y + 1 = 7
3. Ecuación cúbica: Una ecuación cúbica es aquella en la que la variable está elevada al cubo. Por ejemplo:
- x^3 + 2x^2 + x – 1 = 0
- y^3 – 4y^2 + 3y = 6
Es importante destacar que estas son solo algunas ejemplos de ecuaciones completas. Existen muchos otros tipos de ecuaciones con diferentes grados y estructuras. Estas ecuaciones desempeñan un papel fundamental en la resolución de problemas matemáticos y su estudio es esencial en diferentes áreas como la física, la ingeniería y la economía.
PROBLEMA DE ECUACIONES CUADRÁTICAS. Corrección a @danielcarreon
3 métodos para resolver una ecuación cuadrática incompleta | Ejercicio 1
Ejemplos de Ecuación Completa
Ejemplo 1: Ecuación lineal con una incógnita
La ecuación completa es un tipo de ecuación en la que todas las variables y coeficientes están presentes. Consideremos el siguiente ejemplo: 3x + 2 = 8. Aquí, la incógnita es “x” y todos los coeficientes (3 y 2) y términos constantes (8) están presentes. Para resolver esta ecuación, podemos aplicar operaciones algebraicas para aislar la incógnita. Restamos 2 a ambos lados de la ecuación: 3x = 6. Luego, dividimos ambos lados por 3 para obtener el valor de “x”: x = 2.
Ejemplo 2: Ecuación cuadrática
La ecuación cuadrática es un caso especial de la ecuación completa que involucra una variable al cuadrado. Un ejemplo común es x^2 + 5x – 6 = 0. En este caso, tenemos la incógnita “x”, el coeficiente del término cuadrático (1), el coeficiente lineal (5) y el término constante (-6). Para resolver esta ecuación, podemos utilizar el método de factorización, completando el cuadrado o aplicando la fórmula general. Dependiendo del método elegido, obtendremos los posibles valores de “x” que satisfacen la ecuación.
Ejemplo 3: Ecuación cúbica
La ecuación cúbica es otro caso de la ecuación completa, donde la variable está elevada al cubo. Un ejemplo de ecuación cúbica es x^3 + 2x^2 – 5x + 6 = 0. En este caso, tenemos la incógnita “x” y los coeficientes de los términos correspondientes. Resolver una ecuación cúbica puede ser más complicado que resolver una ecuación cuadrática; sin embargo, existen métodos como el método de Cardano-Tartaglia o el método de Horner que pueden utilizarse para encontrar las soluciones reales o complejas.
Ejemplo 4: Ecuación con fracciones
Las ecuaciones completas también pueden involucrar fracciones. Consideremos el siguiente ejemplo: 2/3x – 1/4 = 1/2. Aquí, tenemos la incógnita “x” y todos los coeficientes y términos constantes están expresados como fracciones. Para resolver esta ecuación, podemos multiplicar ambos lados por el denominador común para eliminar las fracciones y luego realizar las operaciones necesarias para aislar la incógnita. En este caso, podemos multiplicar ambos lados por 12 (el denominador común) para obtener una ecuación sin fracciones: 8x – 3 = 6. Finalmente, aislamos la incógnita al sumar 3 a ambos lados y dividir por 8: x = 9/8.
En resumen, las ecuaciones completas son aquellas en las que todas las variables y coeficientes están presentes. Pueden involucrar diferentes tipos de ecuaciones, como lineales, cuadráticas o cúbicas, y pueden incluir fracciones. Resolver una ecuación completa implica aplicar operaciones algebraicas para aislar la incógnita y encontrar su valor. Dependiendo del tipo de ecuación, pueden utilizarse diferentes métodos como factorización, completar el cuadrado o utilizar fórmulas específicas.
Preguntas Frecuentes
¿Cuál es un ejemplo de una ecuación completa en matemáticas y cómo se resuelve?
Un ejemplo de una ecuación completa en matemáticas es la siguiente:
2x + 5 = 13
Para resolverla, debemos despejar la incógnita “x”. Primero, restamos 5 de ambos lados de la ecuación:
2x + 5 – 5 = 13 – 5
Esto nos lleva a:
2x = 8
Luego, queremos despejar “x”, por lo que dividimos ambos lados de la ecuación por 2:
2x / 2 = 8 / 2
Lo cual da como resultado:
x = 4
Por lo tanto, la solución de la ecuación es x = 4.
¿Cómo se construye y se resuelve una ecuación completa en química? Proporciona un ejemplo concreto.
Para construir y resolver una ecuación completa en química, es importante seguir los siguientes pasos:
1. Identificar los reactivos y productos: Observa la reacción química y determina qué sustancias se encuentran antes de la flecha (reactivos) y cuáles se forman después de la flecha (productos).
2. Balancear los átomos: Asegúrate de que la cantidad de átomos de cada elemento sea igual en ambos lados de la ecuación. Para lograr esto, puedes ajustar los coeficientes estequiométricos de las sustancias que intervienen.
3. Balancear las cargas: Si la reacción es una redox, debes asegurarte de que las cargas se conserven en ambos lados de la ecuación. Puedes agregar electrones (e-) para equilibrar las cargas.
4. Verificar el balance: Una vez que hayas ajustado los coeficientes estequiométricos, vuelve a contar los átomos de cada elemento y las cargas para asegurarte de que estén equilibradas.
5. Escribir los estados de agregación y las condiciones de reacción: Opcionalmente, puedes incluir los estados físicos (sólido, líquido, gas o acuoso) y las condiciones (temperatura, presión, catalizadores, etc.) en los que ocurre la reacción.
A continuación, te presento un ejemplo concreto:
Reacción: **Hidróxido de sodio (NaOH) + Ácido clorhídrico (HCl) → Cloruro de sodio (NaCl) + Agua (H2O)**
1. Identificación de reactivos y productos:
– Reactivos: NaOH, HCl
– Productos: NaCl, H2O
2. Balanceo de átomos:
– NaOH + HCl → NaCl + H2O (desbalanceada)
– 2NaOH + HCl → NaCl + 2H2O (balanceada)
3. Balanceo de cargas:
– La reacción no es una redox, por lo que no requiere ajuste de cargas.
4. Verificación del balance:
– Átomos: 2 Na, 2 O, 2 H, 1 Cl, todo está equilibrado.
– Cargas: No se aplican en esta reacción.
5. Estados de agregación y condiciones:
– NaOH (sólido), HCl (acuoso), NaCl (acuoso), H2O (líquido)
Por lo tanto, la ecuación completa y balanceada es:
**2NaOH (s) + HCl (ac) → NaCl (ac) + 2H2O (l)**
¿Cuál es la importancia de las ecuaciones completas en física y cuál es un ejemplo relevante en esta disciplina?
La importancia de las ecuaciones completas en física radica en su capacidad para describir y predecir fenómenos naturales de manera precisa. Estas ecuaciones están constituidas por diferentes variables y constantes que representan las propiedades físicas de un sistema.
Un ejemplo relevante de una ecuación completa en física es la ecuación de movimiento de un objeto en caída libre. Esta ecuación se expresa como:
d = 1/2 * g * t^2
Donde “d” representa la distancia recorrida por el objeto en caída libre, “g” es la aceleración debido a la gravedad y “t” es el tiempo transcurrido.
Esta ecuación completa nos permite calcular la distancia que recorre un objeto en caída libre en función del tiempo y la aceleración debida a la gravedad. Esencialmente, nos brinda una herramienta matemática para comprender y predecir el movimiento de los objetos en situaciones de caída libre.
¿Puede proporcionar un ejemplo de una ecuación completa en el campo de la ingeniería y explicar su aplicabilidad en esta área?
Claro, aquí te dejo un ejemplo de una ecuación completa en el campo de la ingeniería y explicaré su aplicabilidad:
La ecuación de Bernoulli:
La ecuación de Bernoulli es una fórmula utilizada en la mecánica de fluidos, una rama de la ingeniería que estudia el comportamiento de los fluidos en movimiento. Esta ecuación está basada en el principio de conservación de la energía y se utiliza para analizar el comportamiento de los fluidos en sistemas donde hay cambios en la velocidad y altura del fluido.
La ecuación de Bernoulli se expresa de la siguiente manera:
P + 0.5ρv^2 + ρgh = constante
Donde:
– P representa la presión del fluido en un punto dado.
– ρ es la densidad del fluido.
– v es la velocidad del fluido.
– g es la aceleración debido a la gravedad.
– h es la altura del fluido con respecto a un punto de referencia.
Esta ecuación es muy útil en ingeniería, ya que puede ser aplicada en diversas situaciones, como el diseño de tuberías, la aerodinámica de aviones o la hidrodinámica de barcos. Por ejemplo, en el diseño de un sistema de tuberías, la ecuación de Bernoulli puede ayudar a determinar la presión y velocidad del fluido en diferentes puntos del sistema, lo que permite optimizar el diseño y asegurar un flujo eficiente.
En resumen, la ecuación de Bernoulli es una herramienta poderosa en el campo de la ingeniería, ya que permite analizar y predecir el comportamiento de los fluidos en movimiento, lo cual es fundamental para el diseño y optimización de sistemas y maquinarias.
En conclusión, las ecuaciones completas son una herramienta fundamental en el ámbito de las matemáticas y la física, ya que nos permiten describir y resolver de manera precisa fenómenos complejos. A través de los ejemplos presentados, hemos podido comprender su aplicabilidad y utilidad en diferentes contextos. Te invito a compartir este artículo y seguir explorando este fascinante tema. ¡Sigue aprendiendo y descubriendo!