Ejemplos Resueltos de Diagramas de Venn con 3 Conjuntos y Ejercicios

¿Alguna vez te has preguntado cómo visualizar la relación entre tres conjuntos de manera efectiva? El Diagrama de Venn es una herramienta poderosa que permite representar intersecciones y diferencias de forma clara y concisa. En este artículo, exploraremos ejemplos prácticos de diagramas de Venn con tres conjuntos, acompañados de ejercicios resueltos que facilitarán tu comprensión. A través de estas ilustraciones, no solo aprenderás a construir tus propios diagramas, sino que también descubrirás su aplicación en diversos campos del conocimiento.

¡Sigue leyendo para sumergirte en el fascinante mundo de los diagramas de Venn!

### Ejemplos Prácticos de Diagramas de Venn con Tres Conjuntos: Ejercicios Resueltos para Facilitar el Aprendizaje

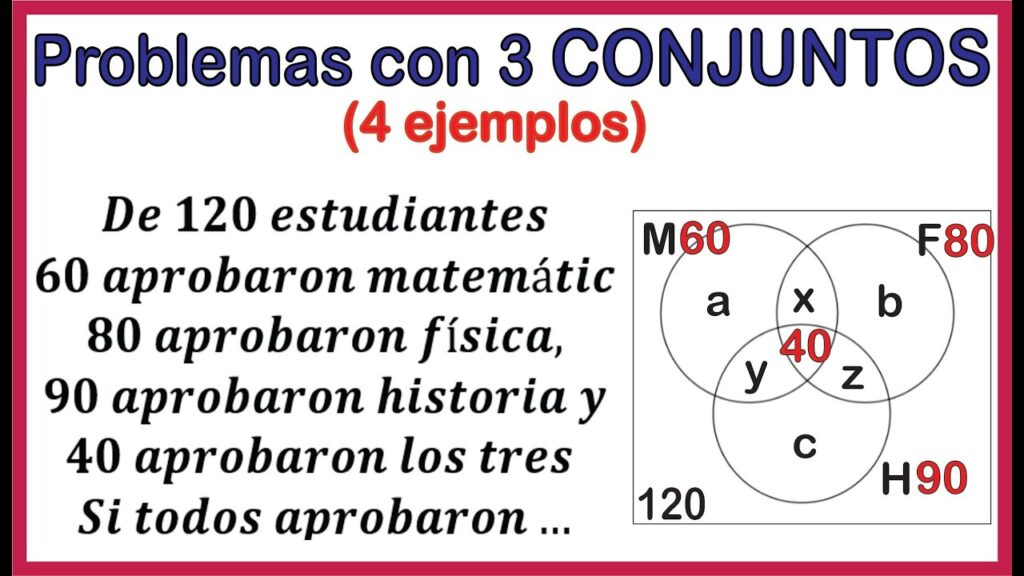
Los diagramas de Venn son herramientas visuales que permiten representar la relación entre diferentes conjuntos. En el caso de tres conjuntos, estos diagramas ofrecen una comprensión clara de cómo se intersecan y se relacionan entre sí. A continuación, se presentan ejemplos prácticos de diagramas de Venn con tres conjuntos y ejercicios resueltos que facilitan el aprendizaje.

Ejemplo 1: Estudiantes en tres asignaturas

Supongamos que tenemos tres conjuntos:

• A: Estudiantes que cursan Matemáticas

• B: Estudiantes que cursan Física

• C: Estudiantes que cursan Química

Imaginemos que los datos sobre los estudiantes son los siguientes:

• 10 estudiantes cursan solo Matemáticas.
• 8 estudiantes cursan solo Física.
• 5 estudiantes cursan solo Química.
• 3 estudiantes cursan Matemáticas y Física, pero no Química.
• 2 estudiantes cursan Matemáticas y Química, pero no Física.
• 4 estudiantes cursan Física y Química, pero no Matemáticas.
• 1 estudiante cursa las tres asignaturas.

Para resolver este ejercicio, primero debemos representar cada uno de los conjuntos y sus intersecciones en el diagrama de Venn. La representación sería la siguiente:

• El área de Matemáticas (A) tendría 10 + 3 + 2 + 1 = 16 estudiantes.
• El área de Física (B) tendría 8 + 3 + 4 + 1 = 16 estudiantes.
• El área de Química (C) tendría 5 + 2 + 4 + 1 = 12 estudiantes.

Al analizar el diagrama, se pueden identificar claramente las intersecciones y la cantidad de estudiantes que pertenecen a cada conjunto y sus combinaciones.

Ejemplo 2: Clasificación de frutas

Consideremos tres conjuntos de frutas:

• X: Frutas tropicales

• Y: Frutas cítricas

• Z: Frutas de hueso

Los datos para este ejemplo son:

• 6 frutas son solo tropicales (por ejemplo, piña, mango).
• 4 frutas son solo cítricas (por ejemplo, naranja, limón).
• 3 frutas son solo de hueso (por ejemplo, ciruela, durazno).
• 2 frutas son tanto tropicales como cítricas (por ejemplo, papaya).
• 1 fruta es tropical y de hueso (por ejemplo, aguacate).
• 1 fruta es cítrica y de hueso (por ejemplo, kumquat).
• 1 fruta es tropical, cítrica y de hueso (por ejemplo, no existe un ejemplo claro, pero se puede considerar un híbrido).

En este caso, al graficar el diagrama de Venn, podemos observar:

• El conjunto de frutas tropicales (X) contiene 6 + 2 + 1 + 1 = 10 frutas.
• El conjunto de frutas cítricas (Y) tiene 4 + 2 + 1 + 1 = 8 frutas.
• El conjunto de frutas de hueso (Z) incluye 3 + 1 + 1 + 1 = 6 frutas.

Estos ejemplos demuestran cómo los diagramas de Venn permiten visualizar y analizar relaciones complejas entre múltiples conjuntos, facilitando así el aprendizaje de conceptos matemáticos y lógicos.

Definición y Características del Diagrama de Venn

¿Qué es un Diagrama de Venn?

El Diagrama de Venn es una representación gráfica que ilustra las relaciones entre diferentes conjuntos. Se utiliza comúnmente en matemáticas, lógica y estadística para visualizar cómo se intersectan o se diferencian varios grupos de elementos. Su inventor, John Venn, presentó esta herramienta en el siglo XIX, y desde entonces ha sido ampliamente aplicada en diversas disciplinas.

Un Diagrama de Venn básico consiste en círculos que se superponen. Cada círculo representa un conjunto, y las áreas donde los círculos se intersectan muestran los elementos comunes entre los conjuntos. Por ejemplo, si tenemos tres conjuntos A, B y C, las intersecciones pueden revelar no solo qué elementos son compartidos entre dos conjuntos, sino también aquellos que pertenecen a los tres.

Características Principales

Las características más relevantes del Diagrama de Venn incluyen:

• Visualización clara: Permite ver rápidamente las relaciones entre los conjuntos.
• Intersecciones: Facilita la identificación de elementos comunes.
• Extensibilidad: Puede adaptarse a cualquier número de conjuntos, aunque los diagramas complejos pueden ser difíciles de interpretar.

Esta herramienta es especialmente útil en situaciones donde se necesita comparar y contrastar diferentes grupos. Por ejemplo, en estudios de mercado, puede ayudar a entender las preferencias de los consumidores en relación a diferentes productos.

Ejemplos Prácticos de Diagramas de Venn con Tres Conjuntos

Ejemplo 1: Animales Domésticos

Consideremos tres conjuntos que representan diferentes tipos de animales domésticos: A (perros), B (gatos) y C (mascotas exóticas).

• El conjunto A incluye todas las razas de perros.

• El conjunto B incluye todas las razas de gatos.

• El conjunto C incluye todas las mascotas exóticas, como reptiles y aves.

En este diagrama, las intersecciones podrían mostrar, por ejemplo, que hay personas que tienen tanto perros como gatos, pero no animales exóticos. Este tipo de visualización ayuda a entender la diversidad y la relación entre las preferencias de mascotas.

Ejemplo 2: Estudiantes y Sus Materias Favoritas

En este caso, consideramos dos conjuntos de estudiantes en una clase: A (estudiantes que prefieren ciencias), B (estudiantes que prefieren humanidades) y C (estudiantes que prefieren deportes).

Al crear un Diagrama de Venn, podemos observar:

• Los estudiantes que solo aman las ciencias.
• Los que se inclinan únicamente hacia las humanidades.
• Los que disfrutan de los deportes.
• Los que combinan intereses en ciencias y humanidades.

Esto permite identificar grupos de estudiantes que comparten intereses académicos y podría influir en la planificación curricular.

Ejercicios Resueltos con Diagramas de Venn

Ejercicio 1: Encuesta de Preferencias de Frutas

Supongamos que realizamos una encuesta sobre preferencias de frutas en un grupo de personas. Los conjuntos son: A (personas que prefieren manzanas), B (personas que prefieren naranjas) y C (personas que prefieren plátanos).

Al analizar los datos, encontramos que:

• 20 personas prefieren manzanas.

• 15 prefieren naranjas.

• 10 prefieren plátanos.

• 5 personas prefieren tanto manzanas como naranjas.

En el Diagrama de Venn, podemos representar estos datos visualmente, mostrando las intersecciones y permitiendo una rápida comprensión de las preferencias de fruta en el grupo.

Ejercicio 2: Actividades Recreativas

Imaginemos un grupo de amigos que disfrutan de diferentes actividades: A (correr), B (nadar) y C (montar en bicicleta).

Si tenemos los siguientes datos:

• 12 amigos corren.

• 10 nadan.

• 8 montan en bicicleta.

• 5 disfrutan de correr y nadar.

Al elaborar un Diagrama de Venn, podemos visualizar claramente cómo se cruzan estas actividades recreativas y qué tan comunes son entre los amigos. Esta información no solo es útil para entender sus preferencias, sino que también puede guiar futuras actividades grupales.

Aplicaciones del Diagrama de Venn en Diferentes Campos

Educación

En el ámbito educativo, el Diagrama de Venn se utiliza para enseñar conceptos de comparación y contraste. Los educadores pueden usarlo para ayudar a los estudiantes a entender las similitudes y diferencias entre temas, personajes literarios o eventos históricos. Esto fomenta el pensamiento crítico y la capacidad de análisis de los alumnos.

Investigación Científica

Los investigadores emplean Diagramas de Venn para ilustrar y organizar datos complejos. Por ejemplo, en estudios de biología, pueden usarse para representar la relación entre diferentes especies o poblaciones y cómo interactúan entre sí. Esto es especialmente valioso al analizar datos de genética o ecología.

Marketing y Negocios

En marketing, los Diagramas de Venn son herramientas útiles para segmentar el mercado. Ayudan a identificar áreas de superposición entre diferentes segmentos de clientes, lo que permite a las empresas personalizar estrategias para atraer a diversos grupos. Esto maximiza la efectividad de las campañas publicitarias y mejora la satisfacción del cliente.

Con el uso adecuado del Diagrama de Venn, se puede mejorar la comprensión de relaciones complejas en múltiples contextos y facilitar la toma de decisiones informadas.

Preguntas Frecuentes

¿Cuáles son los pasos para construir un diagrama de Venn con tres conjuntos utilizando ejemplos prácticos?

Para construir un diagrama de Venn con tres conjuntos, sigue estos pasos:

1. Define los conjuntos: Por ejemplo, considera A (Frutas), B (Rojas), y C (Cítricas).

2. Dibuja el diagrama: Crea tres círculos que se superpongan, cada uno representando uno de los conjuntos.

3. Identifica las intersecciones: Llena cada sección con elementos. Por ejemplo:
– Solo en A: Plátano
– Solo en B: Fresa
– Solo en C: Naranja
– En A y B: Manzana
– En A y C: Limón
– En B y C: Pomelo
– En A, B y C: Grapefruit

4. Revisa la información: Asegúrate de que todos los elementos estén correctamente ubicados según sus características.

Con estos pasos, tendrás un diagrama de Venn claro y funcional.

¿Qué ejercicios resueltos ilustran de manera efectiva la intersección y unión de tres conjuntos en un diagrama de Venn?

Un buen ejemplo para ilustrar la intersección y unión de tres conjuntos en un diagrama de Venn es el siguiente:

Considera los conjuntos A, B y C:

• A: estudiantes que estudian matemáticas.

• B: estudiantes que estudian ciencias.

• C: estudiantes que estudian literatura.

1. Intersección (A ∩ B ∩ C): Representa a los estudiantes que estudian matemáticas, ciencias y literatura al mismo tiempo. En el diagrama, esta área se encuentra en el centro donde los tres círculos se cruzan.

2. Unión (A ∪ B ∪ C): Incluye a todos los estudiantes que estudian al menos una de las materias. Esta área abarca todos los círculos del diagrama.

Estos ejemplos permiten visualizar claramente cómo se relacionan los conjuntos a través de la intersección y la unión.

¿Cómo se pueden aplicar los diagramas de Venn con tres conjuntos en problemas reales de la teoría de conjuntos?

Los diagramas de Venn con tres conjuntos son útiles para visualizar la relación entre diferentes grupos. Por ejemplo, al analizar las preferencias de los consumidores en un mercado, podemos representar a los compradores de productos A, B y C. El área donde se superponen todos los conjuntos indica a los clientes que compran los tres productos, mientras que las áreas exclusivas representan a quienes solo compran uno o dos. Esto ayuda a identificar oportunidades de mercado y a diseñar estrategias de marketing más efectivas.

¿Qué dificultades comunes enfrentan los estudiantes al resolver ejercicios de diagramas de Venn con tres conjuntos y cómo pueden superarlas?

Los estudiantes enfrentan dificultades como confusión en la representación de las intersecciones y errores al identificar elementos pertenecientes a múltiples conjuntos. Para superarlas, es útil practicar con ejemplos concretos, utilizar colores diferentes para cada conjunto y realizar ejercicios en grupo donde se discutan las soluciones. Esto ayuda a clarificar conceptos y mejorar la comprensión.

En conclusión, el diagrama de Venn es una herramienta fundamental para visualizar relaciones entre conjuntos. Los ejemplos y ejercicios resueltos presentados en este artículo facilitan su comprensión y aplicación. Te invitamos a compartir este contenido y a seguir explorando más sobre este tema en nuestro sitio.