¿Te has preguntado alguna vez cómo calcular el área y el perímetro de un círculo? En este artículo, desglosaremos los conceptos fundamentales que rigen estas fórmulas matemáticas esenciales. A través de ejemplos prácticos, descubrirás la importancia de entender estas medidas en diversas aplicaciones, desde la arquitectura hasta la ingeniería.
Acompáñanos en este viaje matemático para dominar el cálculo del círculo y potenciar tus habilidades numéricas de manera efectiva. ¡Comencemos!
Contenido
Ejemplos Prácticos para Comprender el Área y Perímetro del Círculo
El área y el perímetro de un círculo son conceptos fundamentales en geometría que tienen múltiples aplicaciones prácticas. A continuación, se presentan ejemplos que facilitan la comprensión de estos conceptos.
Definición de Área y Perímetro del Círculo
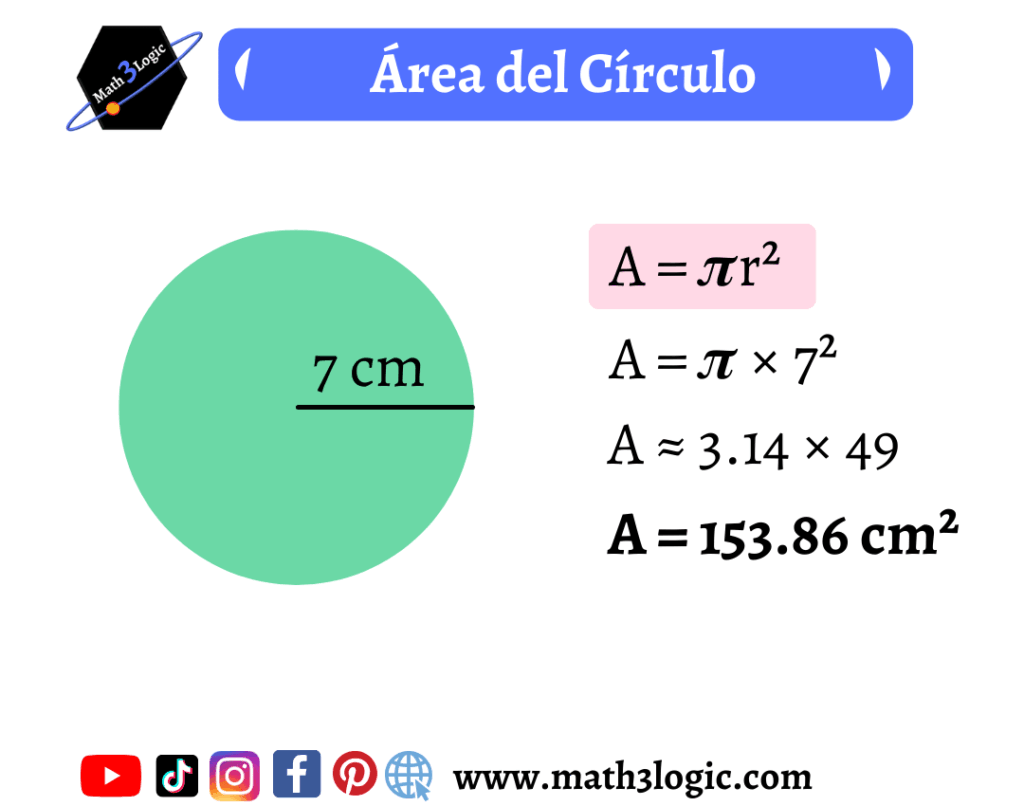
El área de un círculo se define como la cantidad de espacio que ocupa en dos dimensiones y se calcula con la fórmula:
A = πr²
donde “A” es el área y “r” es el radio del círculo. Por otro lado, el perímetro, también conocido como la circunferencia, se refiere a la longitud del borde del círculo y se calcula con la fórmula:
C = 2πr
donde “C” es la circunferencia.
Ejemplo Práctico 1: Cálculo del Área
Consideremos un círculo con un radio de 5 cm. Para calcular el área, aplicamos la fórmula mencionada:
- Identificamos el radio: r = 5 cm.
- Aplicamos la fórmula del área: A = π(5 cm)².
- Calculamos: A = π(25 cm²) ≈ 78.54 cm².
Por lo tanto, el área del círculo es aproximadamente 78.54 cm².
Ejemplo Práctico 2: Cálculo del Perímetro
Ahora, tomemos el mismo círculo con un radio de 5 cm para calcular su perímetro:
- Identificamos el radio: r = 5 cm.
- Aplicamos la fórmula del perímetro: C = 2π(5 cm).
- Calculamos: C = 10π cm ≈ 31.42 cm.
Así, el perímetro del círculo es aproximadamente 31.42 cm.
Ejemplo Práctico 3: Aplicaciones en la Vida Real
Los conceptos de área y perímetro del círculo tienen aplicaciones prácticas en diversas áreas, tales como:
- Arquitectura: Al diseñar espacios circulares, como rotondas o patios, es esencial calcular el área para determinar la cantidad de materiales necesarios.
- Ingeniería: En el diseño de tuberías o tanques, se utiliza el área de la sección transversal circular para calcular capacidades y flujos.
- Jardinería: Al planificar jardines circulares, los jardineros deben calcular el área para saber cuántas plantas pueden ser colocadas en un espacio determinado.
Ejemplo Práctico 4: Comparación de Círculos
Supongamos que tenemos dos círculos, uno con un radio de 3 cm y otro con un radio de 7 cm. Calculemos su área y perímetro:
- Para el círculo de 3 cm:
- Área: A = π(3 cm)² = 9π cm² ≈ 28.27 cm².
- Perímetro: C = 2π(3 cm) = 6π cm ≈ 18.85 cm.
- Para el círculo de 7 cm:
- Área: A = π(7 cm)² = 49π cm² ≈ 153.94 cm².
- Perímetro: C = 2π(7 cm) = 14π cm ≈ 43.98 cm.
Este ejercicio muestra cómo el aumento del radio afecta significativamente tanto el área como el perímetro de un círculo.
Definición de Área y Perímetro en el Círculo
Concepto de Área
El área de un círculo se define como la cantidad de espacio bidimensional que ocupa. Se calcula utilizando la fórmula ( A = pi r^2 ), donde ( A ) representa el área y ( r ) es el radio del círculo. Esta fórmula resulta fundamental en diversas aplicaciones, desde la geometría básica hasta la ingeniería y la física.
Concepto de Perímetro
El perímetro de un círculo, también conocido como circunferencia, se refiere a la longitud del borde del círculo. La fórmula para calcularlo es ( P = 2pi r ). Al igual que el área, el perímetro tiene múltiples aplicaciones prácticas, como en la construcción y el diseño gráfico.
Ejemplos Prácticos del Cálculo del Área
Ejemplo con un Círculo de Radio 5 cm
Supongamos que tenemos un círculo con un radio de 5 cm. Para calcular su área, utilizamos la fórmula mencionada anteriormente:
- Identificamos el radio: ( r = 5 , cm )
- Aplicamos la fórmula: ( A = pi (5)^2 )
- Realizamos la operación: ( A = pi times 25 approx 78.54 , cm^2 )
Por lo tanto, el área de este círculo es aproximadamente 78.54 cm², lo que nos indica la superficie que ocupa.
Ejemplo con un Círculo de Radio 10 m
Consideremos ahora un círculo con un radio de 10 m. El procedimiento es similar:
- Identificamos el radio: ( r = 10 , m )
- Aplicamos la fórmula: ( A = pi (10)^2 )
- Calculamos: ( A = pi times 100 approx 314.16 , m^2 )
De esta manera, el área de este círculo es aproximadamente 314.16 m².
Ejemplos Prácticos del Cálculo del Perímetro
Ejemplo con un Círculo de Radio 5 cm
Siguiendo con el círculo de radio 5 cm, calculamos su perímetro:
- Identificamos el radio: ( r = 5 , cm )
- Aplicamos la fórmula: ( P = 2pi (5) )
- Realizamos la operación: ( P = 10pi approx 31.42 , cm )
Así, el perímetro de este círculo es aproximadamente 31.42 cm.
Ejemplo con un Círculo de Radio 10 m
Ahora, calculemos el perímetro de un círculo con un radio de 10 m:
- Identificamos el radio: ( r = 10 , m )
- Aplicamos la fórmula: ( P = 2pi (10) )
- Calculamos: ( P = 20pi approx 62.83 , m )
Por lo tanto, el perímetro de este círculo es aproximadamente 62.83 m.
Relación entre Área y Perímetro
Proporcionalidad y Comparaciones
Es interesante notar que el área y el perímetro de un círculo están interrelacionados, aunque no directamente proporcionales. A medida que aumenta el radio de un círculo, tanto su área como su perímetro también aumentan, pero no al mismo ritmo. Por ejemplo, si duplicamos el radio, el área se cuadruplica, mientras que el perímetro solo se duplica.
Aplicaciones de la Relación
Esta relación es relevante en campos como la arquitectura, donde se busca maximizar el espacio (área) mientras se controla la cantidad de material utilizado (perímetro). Las decisiones de diseño a menudo dependen de encontrar un equilibrio entre estas dos dimensiones.
Errores Comunes en el Cálculo del Área y Perímetro
Errores en la Fórmula
Uno de los errores más comunes es confundir las fórmulas del área y el perímetro. Es crucial recordar que el área involucra el cuadrado del radio, mientras que el perímetro implica simplemente el radio multiplicado por constantes.
Errores de Unidad
Otro error frecuente es no prestar atención a las unidades. Al calcular el área, las unidades son cuadradas (cm², m²), mientras que el perímetro se expresa en unidades lineales (cm, m). Confundir estas unidades puede llevar a resultados incorrectos y conclusiones erróneas en aplicaciones prácticas.
Preguntas Frecuentes
¿Cuáles son algunos ejemplos prácticos de cálculo del área y perímetro de un círculo en situaciones cotidianas?
Algunos ejemplos prácticos de cálculo del área y perímetro de un círculo en situaciones cotidianas incluyen:
1. Jardines redondos: Si deseas plantar un jardín circular, puedes calcular el área para saber cuántas plantas caben y el perímetro para comprar bordes o cercas.
2. Ruedas de vehículos: Al medir una rueda, el perímetro (circunferencia) te ayuda a entender la distancia que recorrerá en cada vuelta, mientras que el área podría ser útil para calcular el espacio ocupado por un neumático.
3. Pizarras o mesas redondas: Calcular el área permite saber cuántos materiales caben sobre la superficie, y el perímetro puede ayudar en la elección de manteles o cubiertas.
4. Círculos en deportes: En deportes como el baloncesto, el diámetro de la cancha se puede utilizar para calcular el perímetro de la zona restringida y el área para establecer estrategias de juego.
¿Cómo se aplican las fórmulas del área y perímetro del círculo en problemas de geometría analítica?
Las fórmulas del área y el perímetro del círculo, A = πr² y P = 2πr, se aplican en problemas de geometría analítica para calcular características de círculos situados en el plano cartesiano. Por ejemplo, si se tiene un círculo con centro en (h, k) y radio r, se puede determinar su ecuación como (x – h)² + (y – k)² = r². A partir de aquí, se pueden calcular tanto el área como el perímetro usando las fórmulas mencionadas, facilitando así la resolución de problemas que involucran intersecciones, distancias y áreas en el plano.
¿Qué ejemplos ilustrativos pueden ayudar a entender la relación entre el diámetro, radio, área y perímetro de un círculo?
Un ejemplo ilustrativo es pensar en una pizza. Si la pizza tiene un diámetro de 12 pulgadas, el radio es la mitad, es decir, 6 pulgadas. El perímetro (o circunferencia) se calcula como 2πr, que sería aproximadamente 37.7 pulgadas. El área se calcula como πr², resultando en alrededor de 113.1 pulgadas cuadradas. Así, al visualizar la pizza, se comprende cómo estos conceptos están interrelacionados.
¿Se pueden encontrar ejemplos de áreas y perímetros de círculos en contextos arquitectónicos o de diseño?
Sí, se pueden encontrar ejemplos de áreas y perímetros de círculos en contextos arquitectónicos y de diseño. Por ejemplo, el diseño de rotondas en urbanismo utiliza el cálculo del área para determinar el espacio verde necesario. Asimismo, en la creación de ventanas circulares, se aplica el perímetro para definir marcos y estructuras adecuadas.
En conclusión, comprender el área y el perímetro del círculo a través de ejemplos prácticos es fundamental para dominar conceptos geométricos. Estos conocimientos no solo son aplicables en matemáticas, sino también en diversas disciplinas. Te invitamos a compartir este contenido y a seguir explorando más temas relacionados. ¡Tu aprendizaje continúa aquí!